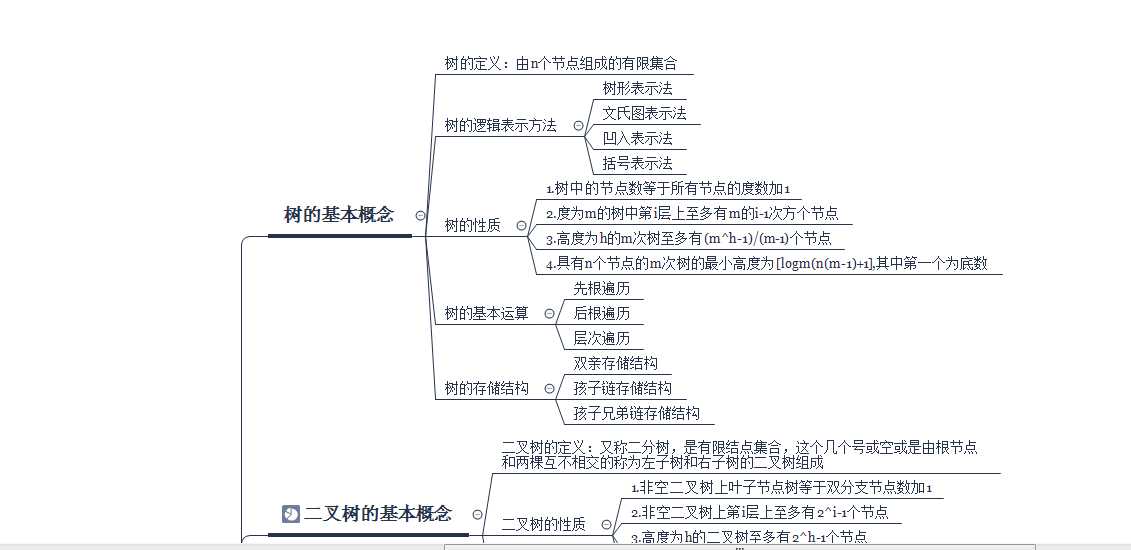


对于本章树结构的学习,我觉得对于自己来说难度比前面的学习要更大,在做题的时候总是弄不清楚树中节点,父母亲,孩子的各种关系操作,有时候觉得有点抽象,对于书上的代码有一些也不是完全能理解,还是要再对树这节花很多的时间了
建树,将二叉树的顺序存储结构转换为链式存储结构
BTNode *bt;
if i大于字符串长度或小于0
返回NULL;
if 节点不存在,
返回NULL
创建根节点
记录各节点的长度bt->k=log(i)/log(2)+1;
递归创建左子树bt->lchild =CreateBTree(str,2*i);
递归创建右子树bt->rchild =CreateBTree(str,2*i+1);
返回bt
end求叶子节点的WPL
if 树为空
返回0
找到叶子节点
sum1=sum1+(bt->data-‘0‘)*(bt->k-1);
递归求出左子树叶子节点的WPL
递归求出左子树叶子节点的WPL
返回 sum1
end 

一开始时将记录叶子节点长度b->k放到WPL函数中,这时记录的是最底层叶子节点的长度,求不出树中的其他叶子节点的长度,并且sum1定义在WPL函数中,这样每次递归后sum1的一开始都会置于0,导致递归失败;
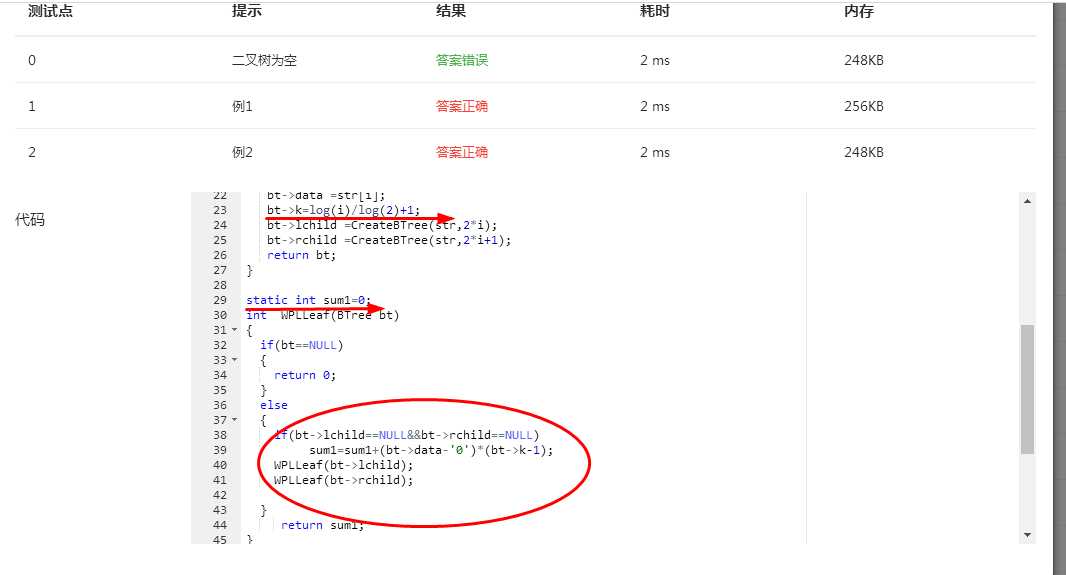
后来改为上述后,答案正确,但是还是有测试点未过
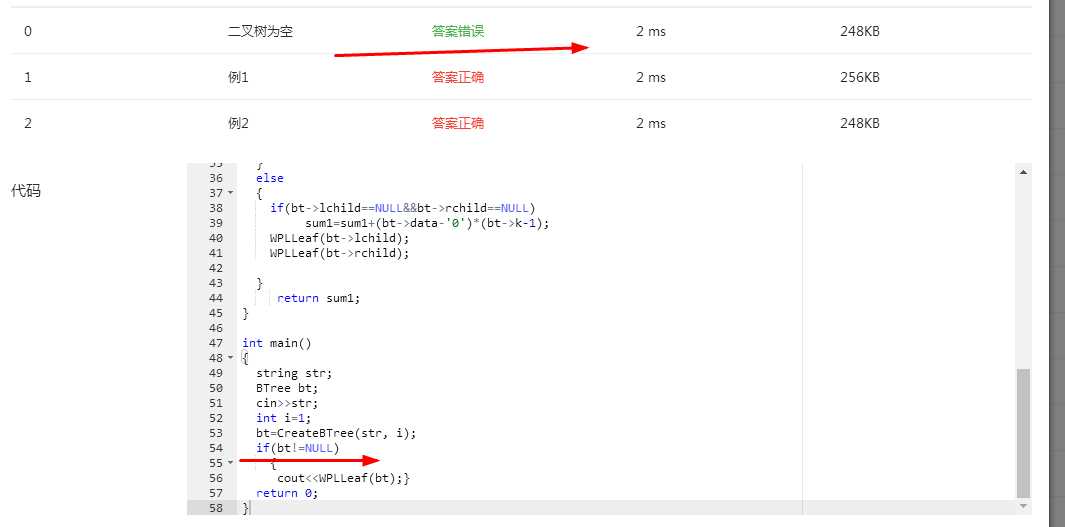
没有考虑到如果树为空,应输出0;
定义total,n;
输入n;
调用priority_queue<int,vector<int>,greater<int> >que;//调用此函数,可将输入的数据做升序处理
循环输入长度k,que.push(k);
while(que.size()>1){
取栈中两较小元素
total+=a+b;
que.push(a+b);
}
输出total
end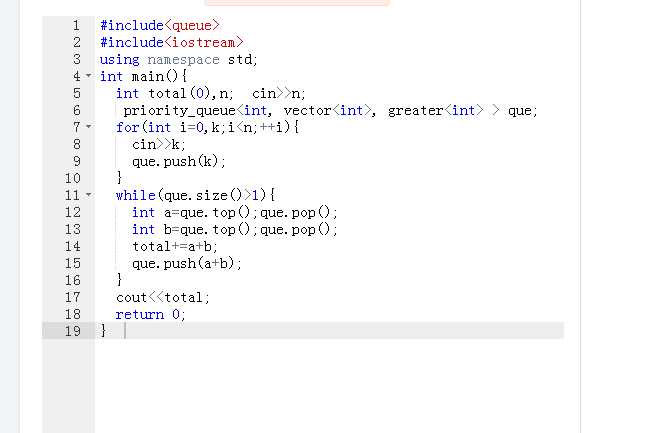
一开始的时候是采用数组做的,其思路就是将木块的各个长度存放于数组中,然后做升序处理,在从数组中取出两较小元素相加后,将此结果再次插入取出后的数组中,仍保持有序,循环处理遍历完数组,最后输出的相加的结果就是最少的花费,这样做可以实现题目的要求,但是pta上却是显示答案错误,
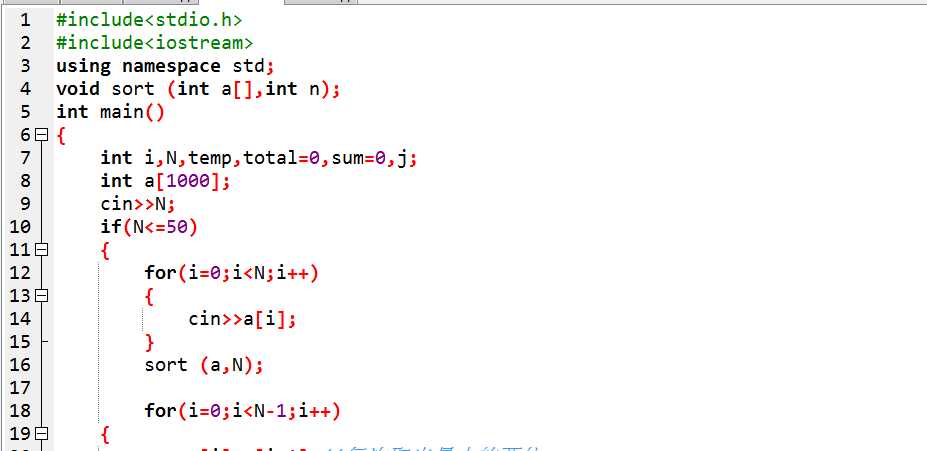
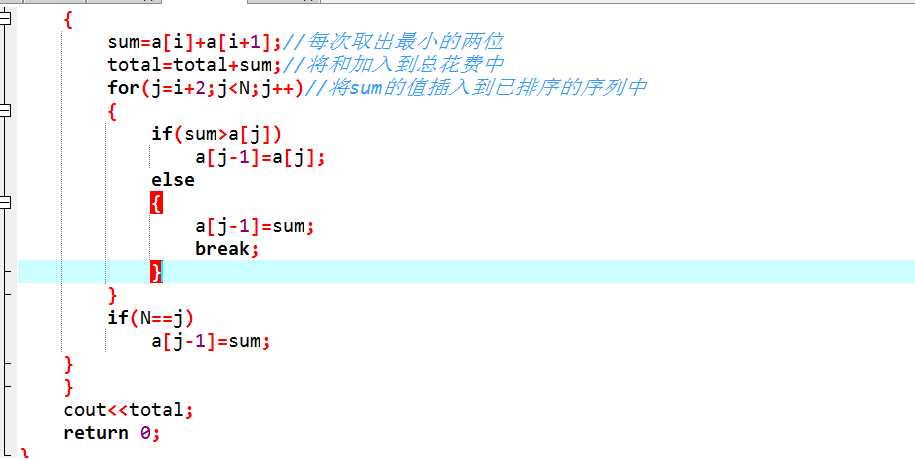


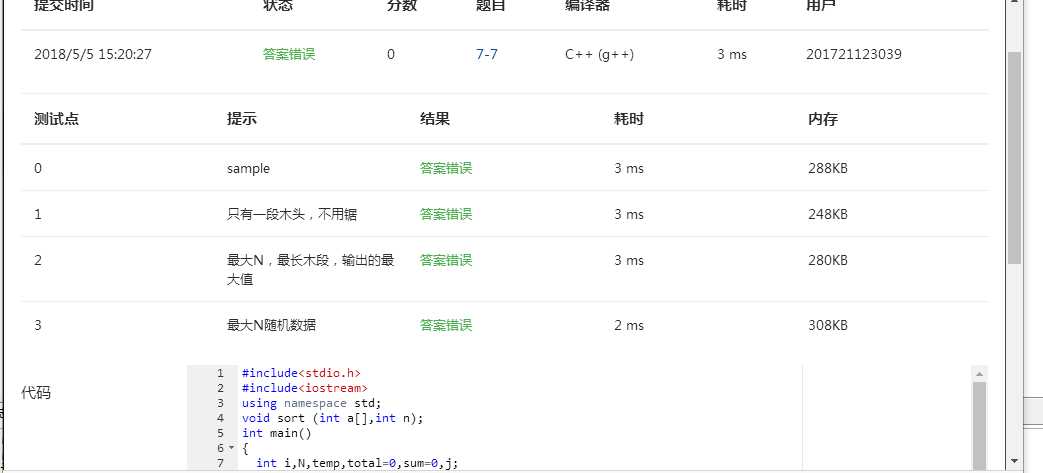
后来在网上看到说可以调用priority_queue


此题为构造哈夫曼树,然后求出WPL,做这题一开始想得是每次选择两个数据相加后马上进行一次快速排序。其实每次相加后是一个相对有序的数组,用快排是不合适的,但是上述代码调用了priority_queue<int, vector
原文:https://www.cnblogs.com/2223ch/p/8995270.html