
树的操作普遍用到了递归,自己在这方面上有点薄弱,所以得理解比较久。如果不用上递归也是要借助
栈,队列等工具。这一块得内容比较多,得多花时间。特别是树得基本内容,各种结点,创建树等都要掌握
好。基础弄懂才能比较好的运用,现在做起题目还是比较吃力,还是得继续努力。
如果树为空 return 0;
递归遍历左右子树;
比较两边的高度,返回值比较大的一个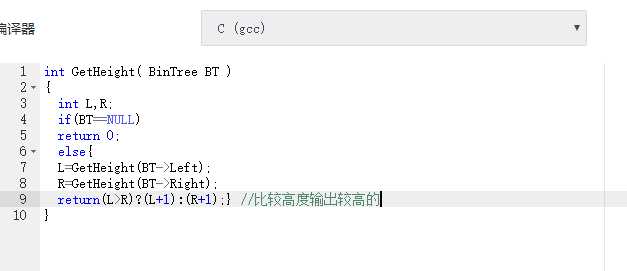

本题没有碰到问题。
创立两个栈一个放树,一个放操作符
for i=0 to str[i]
如果str[i]不是操作符
建立一个结点
把它入栈
如果它是操作符
while(栈顶的操作符比碰到的操作符优先级大)
{
分别取出树栈中两个元素作为左右孩子
创立新的树
再入栈该树}
while(栈顶的操作符比碰到的操作符优先级一样)
{
把操作符栈出栈一个
continue}
while(操作符栈不为空)
{
分别取出树栈中两个元素作为左右孩子
创立新的树
再入栈该树}
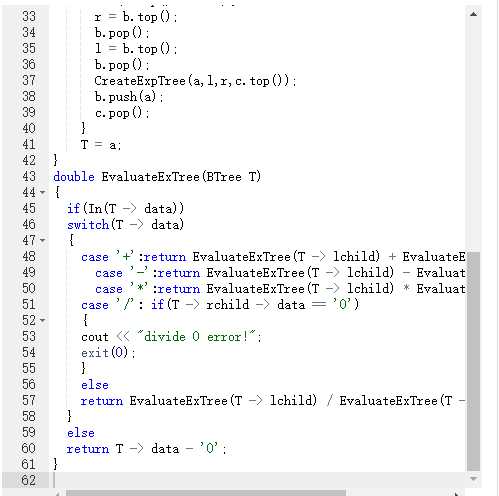
开始时对于进栈和出栈的操作有问题,询问同学后进行了改正。
层次遍历:
定义一个环形队列
如果树并不为空就把它入对
while(队列不为空)
{
取出队列的第一个元素
输出该结点对应的值
如果(该结点对应左子树不为空)
就把该左子树入队
如果(该结点对应右子树不为空)
就把该右子树入队
}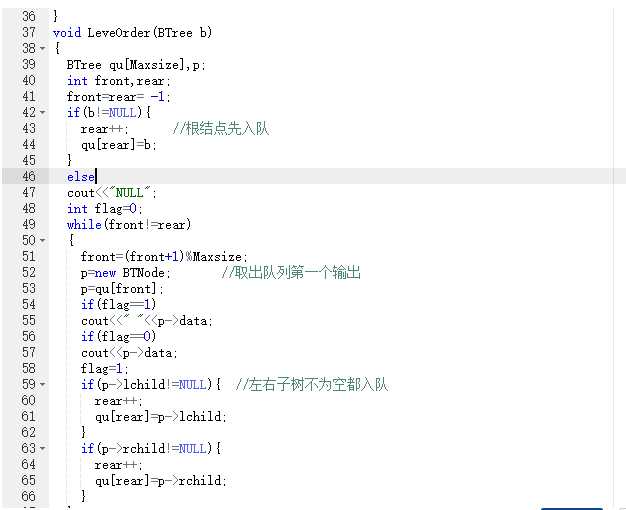

答案错误:设置的测试点未删除,导致输出有问题。
部分正确:在建树上面出了点问题---求字符长度判断未减一;后进行了改正。
3.1 PTA排名
void levelOrderTraverse(const BiTree& T)
{
queue<BiTree> q;
BiTree p = NULL;
if(T)//若根结点非空,则入队列
{
q.push(T);
}
while(!q.empty())//队列非空
{
p = q.front();
q.pop();
cout<<p->data<<" ";
if(p->lchild)//左孩子不空,入队列
{
q.push(p->lchild);
}
if(p->rchild)//右孩子不空,入队列
{
q.push(p->rchild);
}
}
} 该代码是实现层次遍历的功能,自己的做法是用书里建立环形队列的方法
该代码用的是普通队列,直接看的话还是该代码比较简洁,而且更易理解。
原文:https://www.cnblogs.com/lzc176/p/8995391.html