转载请标明出处:http://www.cnblogs.com/tiaozistudy/p/anomaly_detection.html
本文主要针对IBM SPSS Modeler 18.0中离群点检测算法的原理以及“异常”节点(见图1)使用方法进行说明。SPSS Modeler中的离群点检测算法思想主要基于聚类分析。如图2所示,可先将图中样本点聚成三类,$A$、$B$和$C$三个样本点应分别属于距离他们最近的类,但与相对类内的其他样本点,这三个点又分别远离各自的类,所以可以基于此判定是离群点。

图1:“异常”节点
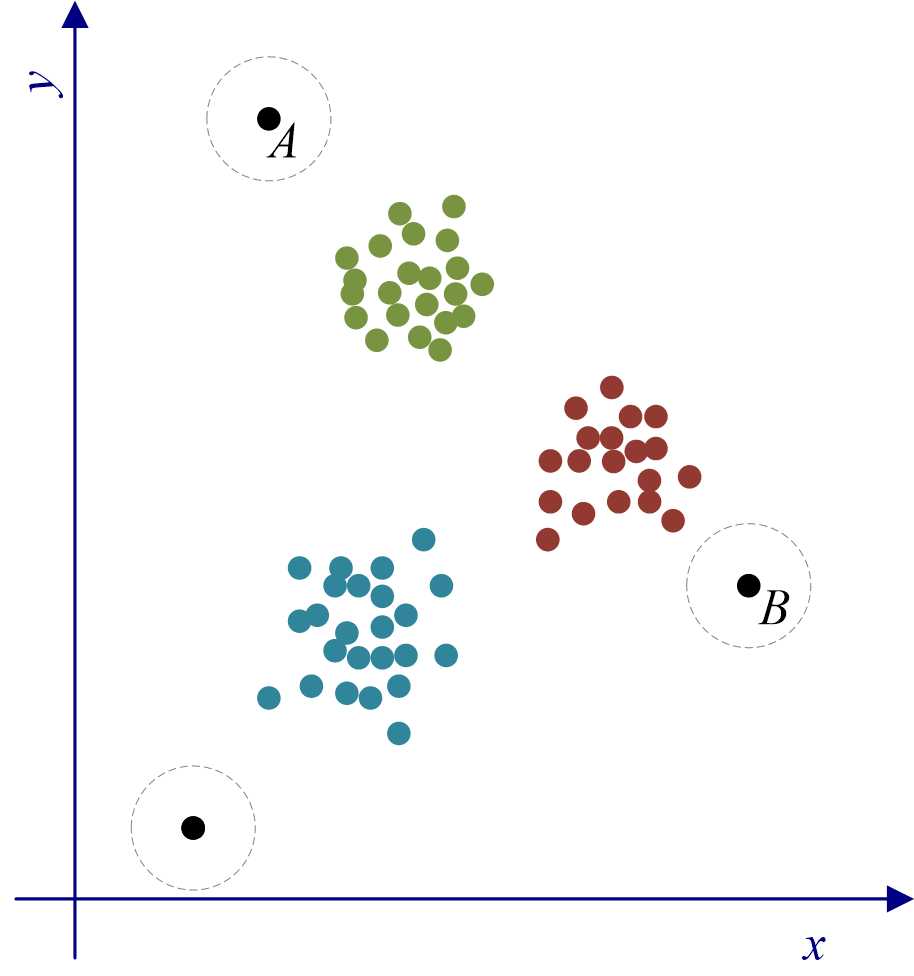
图2:离群点检测示意图
根据上述分析,你群点检测算法主要分为三个阶段:第一阶段,聚类,即将样本点聚成若干类;第二阶段,计算,即在第一阶段聚类的基础上,依据距离计算所有样本点的异常性测度指标;第三阶段,诊断,即在第二阶段异常性测度指标的基础上,确定最终的离群点,并分析导致样本点异常的原因,也就是分析离群点在哪个变量方向上呈现异常。以下就这三个阶段分别讨论:
该阶段主要借助两步聚类算法实现对所有样本点的聚类(可参考两步聚类算法的相关内容)。两步聚类算法主要分为两个步骤:第一步是通过构造聚类特征(CF)树将大量零散的数据样本浓缩成可管理数量的子簇;第二步是从CF树叶节点的子簇开始利用凝聚法(agglomerative hierarchical clustering method),逐个地合并子簇,直到期望的簇数量。
两步聚类算法可以进行离群点处理,首先在CF树瘦身(rebuilding)之前筛选出潜在离群点,并CF树瘦身步骤后重新插入误识离群点到中。
在完成数据集中所有数据样本到CF树上的插入后,仍为潜在离群点的元项,视为最终离群点。这些离群点将会分配到第二步凝聚法的聚类结果中。
“异常”节点中与此阶段相关的,是其“专家”选项的相关参数设计(见图3):
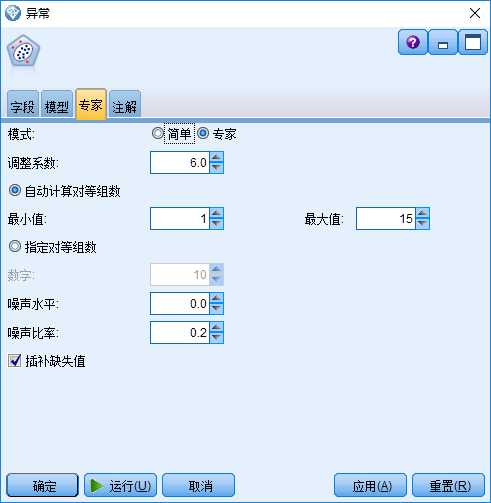
图3:“异常”节点的“专家”选项
第二阶段的任务是在第一阶段聚类的基础上,计算样本的异常性测度指标,异常性测度指标的计算是基于对数似然距离(可参考对数似然距离的相关内容)。对于样本点$s$,离群点检测算法计算了以下指标。
(1)找到样本点$s$所属的簇$C_j$。通过计算$\{s\}$与$C_j \setminus \{s\}$的对数似然距离得到样本点$s$的组差异指标GDI(Group Deviation Index):
\begin{equation}\label{Eq.1}
GDI_s = d(\{s\}, C_j \setminus \{s\}) = \zeta_{C_j \setminus \{s\}} + \zeta_{\{s\}} - \zeta_{C_j}
\end{equation}
其中
\begin{equation*}
\zeta_{C_j} = -N_j \left ( \frac12 \sum_{k=1}^{D_1} \ln (\hat \sigma^2_{jk} + \hat \sigma^2_k) + \sum_{k=1}^{D_2} \hat E_{jk} \right )
\end{equation*}
\begin{equation*}
\hat E_{jk} = -\sum_{l=1}^{\epsilon_k} N_{jkl}/N_j \ln (N_{jkl}/N_j)
\end{equation*}
公式中符号的具体含义见“对数似然距离”。GDI反映的是,样本点$s$加入簇$C_j$后所引起的簇$C_j$内部差异/散布的增大量,因此GDI越大,样本点越有可能是离群点。
(2)根据$\zeta_{C_j}$的定义,$\zeta_{C_j}$可以划分成各变量上值得线性组合:
\begin{equation*}
\zeta_{C_j} = \sum_k^D \zeta_{C_j}^{(k)}
\end{equation*}
其中
\begin{equation*}
\zeta_{C_j}^{(k)} =
\begin{cases}
- \frac{N_j}2 \ln (\hat \sigma^2_{jk} + \hat \sigma^2_k), & \text{变量}k\text{是连续型的} \\
-\sum_{l=1}^{\epsilon_k} N_{jkl} \ln (N_{jkl}/N_j), & \text{变量}k\text{是分类型的}
\end{cases}
\end{equation*}
进一步定义样本点$s$在变量$k$上的变量差异指标VDI(Variable Deviation Index):
\begin{equation}\label{Eq.2}
VDI_s^{(k)} = \zeta_{C_j \setminus \{s\}}^{(k)} + \zeta_{\{s\}}^{(k)} - \zeta_{C_j}^{(k)}
\end{equation}
因此有$GDI_s = \sum_k VDI_s^{(k)}$,变量差异指标VDI表示各变量在组差异指标GDI上的“贡献”大小。
(3)计算异常指标AI(Anomaly Index)。
对于样本点$s$,其AI定义为:
\begin{equation}\label{Eq.3}
AI_s = \frac{GDI_s}{\frac{1}{|C_j|} \sum_{t \in C_j} GDI_t}
\end{equation}
AI是一个相对指标较GDI更直观,是样本点$s$所引起的簇内差异与簇$C_j$内其它样本点所引起差异的平均值的比例,该值越大,认为样本点$s$是离群点的可能性就越大。
(4)计算变量贡献指标VCM(Variable Contribution Measures)。
对于样本点$s$,变量$k$的贡献指标定义为
\begin{equation}\label{Eq.4}
VCM_s^{(k)} = \frac{VDI_s^{(k)}}{GDI_s}
\end{equation}
VCM是一个相对指标,较VDI更直观,反映的是各聚类变量对组内差异“贡献”的比例。该值越大,则相应变量导致样本点$s$离群原因的可能性越大。
第二阶段计算得到了所有样本点的GDI、VDI、AI和VCM,本阶段将依据这些指标的排序结果,确定离群点,并分析导致异常的原因。
“异常”节点中与第二、三阶段相关的,是其“模型”选项的相关参数设计(见图4):
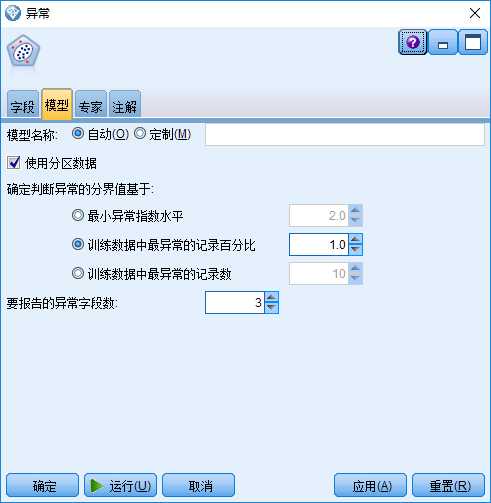
图4:“异常”节点的“模型”选项
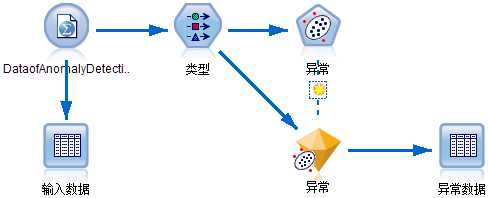
图5:异常检测示例流
参考《SPSS Modeler数据挖掘方法及应用》中的数据和流,构造了图5中所示的流。打开流中的模型块(如图6和7所示)。
图6中“模型”选项的结果表明,所有样本数据聚成了两类(称之为“对等组”),第1类包含498个样本,发现5个离群点;第2类包含169个样本,发现1个离群点。对第1类中5 个离群点分别找出3个VCM值(见式(4))最大的变量,形成了图6中的上表。所有5个离群点对应的3个VCM值最大的变量中都包含“基本费用”,换句话说,变量“基本费用”对于形成所有5个离群点都有较大贡献,5个离群点的平均VCM 值为0.165. 另一个需要注意的变量是“免费部分”,虽然该变量只对3个离群点的成因有较大贡献,但其平均VCM的值达到了0.325,这说明,它对这3个离群点的成因有非常大的贡献。
图7中“摘要”选项给出了判断离群点的AI阈值,即“异常指数分界值:1.52328”。 针对本次找出的6个离群点,通过式(3)计算出的AI值都不小于该值,而其它样本点的AI值都小于该值。
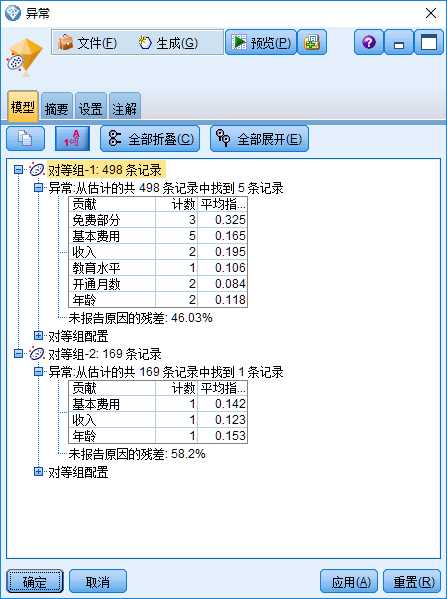
图6:“异常”模型块的“模型”选项
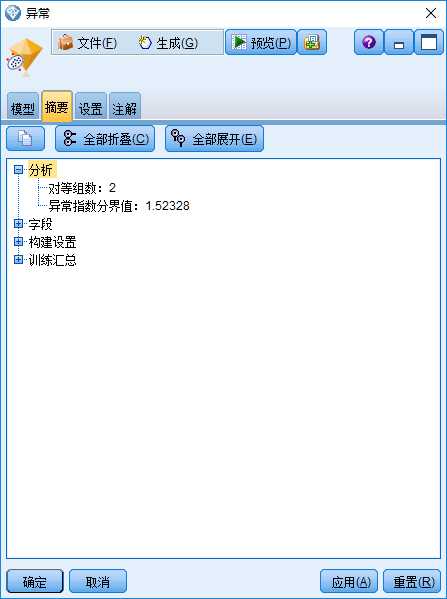
图7:“异常”模型块的“摘要”选项
在模型块的“设置”选项中选中“丢弃记录”-“非异常”后运行“异常数据”表格,得到如图8的离群点输出结果,该表格中一共出现了5类新变量:
表1:新变量说明
| 新变量名称 | 说明 |
| $O-Anomaly | 是否离群点,T:是,F:否 |
| $O-AnomalyIndex | 该样本的异常指标AI,由式(3)计算 |
| $O-PeerGroup | 样本分配到的对等组(所在簇) |
| $O-Field-n | VCM第n大的变量名称,VCM由式(4)计算 |
| $O-FieldImpact-n | VCM第n大的变量对应的VCM值 |
以图5中的流为例,因为图4中的“要报告的异常字段数”设定为3,所以$O-Field-n和$O-FieldImpact-n中的$n$最大只能取到3. 再看图8中的第一行,该样本的$AI=1.530$,属于第一个簇,VCM贡献最大的变量是“收入”,该样本在变量“收入”下的$VCM=0.200$.
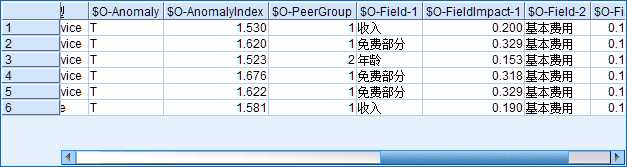
图8:离群点输出结果表
[1] 薛薇, 陈欢歌. SPSS Modeler数据挖掘方法及应用[M]. 北京: 电子工业出版社. 2014.
原文:https://www.cnblogs.com/tiaozistudy/p/anomaly_detection.html