描述
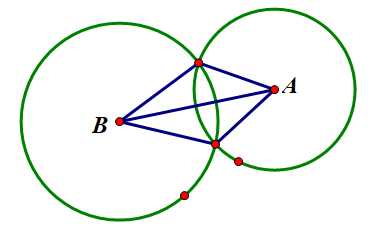
There are two circles on the plane. Now you must to calculate the area which they cover the plane. For example, in Figure 1, the area of the red region is the answer of this problem.

输入
The input contains multiple test cases. The first line contains an integer T describing the number of test cases. Each case contains two lines. One line describes one circle. For each line has three integers x, y, r, indicating the coordinate of the centre and radius. All the numbers are separated by spaces. All the input integers are within the range of [-1000, 1000].
输出
For each test case, output one line containing a number with 3 digits after decimal point representing the answer describing above.
样例输入
2
2 2 2
1 4 3
2 2 1
-2 -2 1
样例输出
32.462
6.283
题解
就是用两个圆形面积之和-(两个扇形面积之和减去两个大三角形的面积)
#include<bits/stdc++.h> #define pi acos(-1.0) using namespace std; int main() { int t; double x1,y1,r1,x2,y2,r2,s,d,a1,a2,s1,s2,shan1,shan2; cin>>t; while(t--) { cin>>x1>>y1>>r1>>x2>>y2>>r2; d=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); if(r1>r2) swap(r1,r2),swap(x1,x2),swap(y1,y2); s1=pi*r1*r1; s2=pi*r2*r2; if(d>=r1+r2) s=s1+s2; else if(d<=r2-r1) s=s2; else { double coshalfA=(r1*r1+d*d-r2*r2)*1.0/(2*r1*d); double A=acos(coshalfA)*1.0/pi*180*2; shan1=A*pi*r1*r1/360.0; a1=r1*r1*0.5*sin(A*pi/180); double coshalfB=(r2*r2+d*d-r1*r1)*1.0/(2*r2*d); double B=acos(coshalfB)/pi*180*2; shan2=B*pi*r2*r2*1.0/360; a2=r2*r2*0.5*sin(B*pi/180); s=s1+s2-(shan1+shan2-a1-a2); } printf("%.3f\n",s); } return 0; }
原文:https://www.cnblogs.com/kannyi/p/9011635.html