内容摘要:
素数(prime number)到底是啥数:
定义:
在大于1的自然数中,除了1和它本身以外不能再被其他数所整除。
实例化定义:
需要注意:
埃式筛法是干什么用的:
作用:
从一堆自然数里面,找出这一堆自然数里面的所有的素数。
实例化:
利用java实现埃式筛法的思路:
首先明确算法主要的依据以及两个前提:
主要的依据:任何一个合数,一定有比他小的素数因子。(大家可以利用小时候学的分解自然数的过程去理解一下这句话)
下面是寻找n = 50以内的所有素数的实例:
我们首先建立了一个数字由2到50的数组。
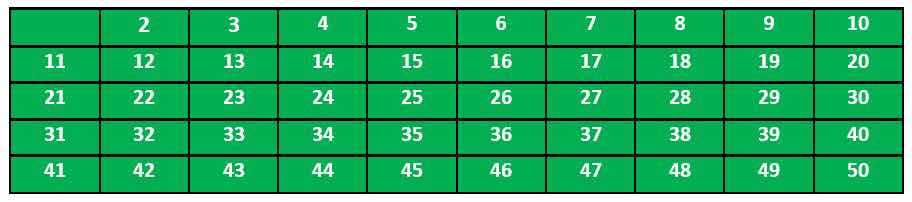
然后我们确定2是素数,所以我们标记了所有2的倍数为非素数。
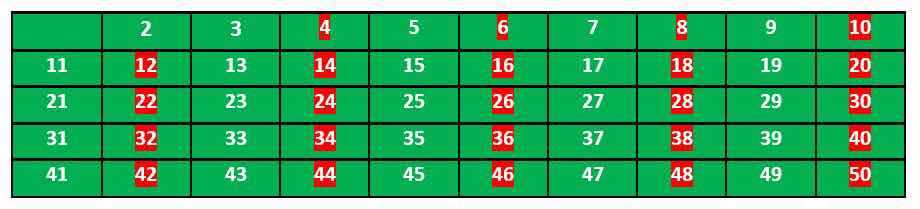
因为3没有在上一步被标记,所以我们得出3是素数,然后我们标记所有3的倍数为非素数
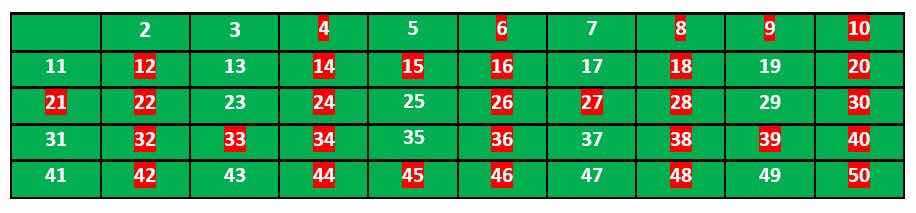
然后我们来到没有被标记的数字5,然后标记所有5的倍数为非素数
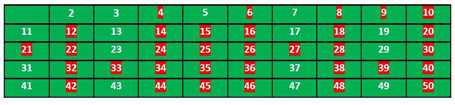
我们继续,然后得到
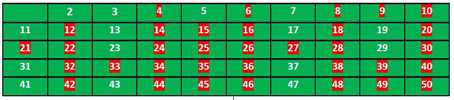
所以,素数应该是这里面没有被标记的元素:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47.
(以上Figure由Krishan Kumar提供)
转化成代码的几个关键部分:
1.利用boolean类型的素组去标记非素数
2.算法由嵌套的两层循环组成
java代码(找出自然数upperBound内,包括upperBound的所有的素数,并且把它们输出)
1 public void runEratosthenesSieve(int upperBound) {
2 int upperBoundSquareRoot = (int) Math.sqrt(upperBound);
3 /*这里取平方是因为通过数学推理可以知道只需要判断到upperBound的上界即可。
4 第一次写的读者可以把循环的次数设置成upperBound,便于理解*/
5 boolean[] isComposite = new boolean[upperBound + 1];
6 //这个boolean类型的数组是为了标记upperBound以内的自然数
7
8 for (int m = 2; m <= upperBoundSquareRoot; m++) {
9 if (!isComposite[m]) {
10 System.out.print(m + " ");
11 for (int k = 2 * m; k <= upperBound; k += m)
12 isComposite[k] = true;
13 }
14 }
15 for (int m = upperBoundSquareRoot; m <= upperBound; m++)
16 if (!isComposite[m])
17 System.out.print(m + " ");
18 }

题意:输出第M~N个素数。
思路:利用筛法把素数表打印至第N个素数,然后按格式输出。
java代码
1 class Prime1{ 2 private int maxn =100010; 3 private int a[] =new int[maxn]; 4 5 void isPrime(int n){ 6 boolean flag[] = new boolean[maxn]; 7 int index=0; 8 for(int i=2;i<maxn;i++){ 9 if(index>=n) break;//无需找出第n个素数后的素数 10 if(! flag[i]){ 11 a[index]=i; 12 index++; 13 for (int j=2*i;j<maxn;j+=i){ 14 flag[j]=true; 15 } 16 } 17 } 18 } 19 20 void outprint(int m,int n){ 21 int count=0; 22 isPrime(n); 23 for(int i=m-1;i<n;i++){ 24 if(count%10!=0&&i!=n-1){ 25 System.out.print(a[i]+" "); 26 }else{ 27 System.out.println(); 28 } 29 } 30 } 31 }
改进筛法:
*我们注意到,算法中标记倍数可以从已找到的素数的平方开始标记(而不是从它的两倍开始)
对于 m = 2,原先的算法标记了
2*2 3*2 4*2 5*2 6*2 7*2 8*2 ...
对于 m = 3,原先的算法标记了
2*3
2*3这一步在m = 2的时候已经被标记
对于 m = 5,
2*5 3*5 4*5(= 10*2)
已经在m = 2以及m = 3的时候被标记了
这里缺少了严格的数学证明,有兴趣的读者朋友可以自己证明。
对范围在2~100的数应用改进后埃式筛法筛选出这里面的所有素数的过程:
装有2~100自然数的数组的最初状态。
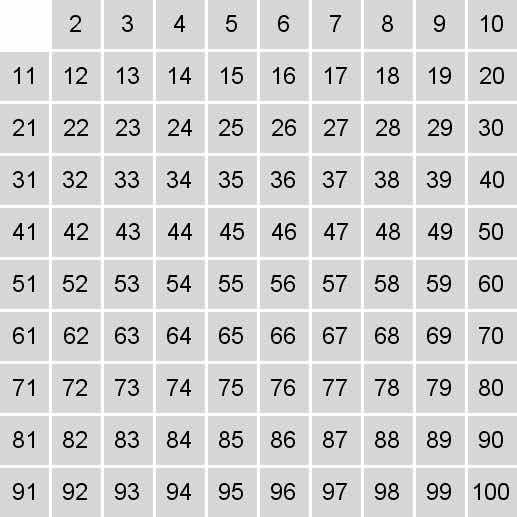
2是素数,标记所有2的倍数。从4开始。
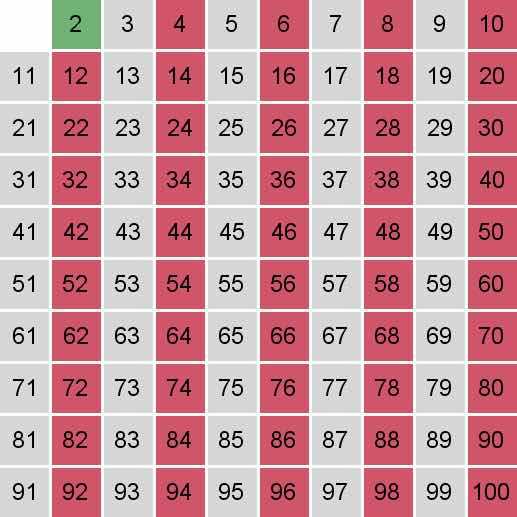
3在上一步没有被标记,所以3是素数。标记所有3的倍数,从9开始。
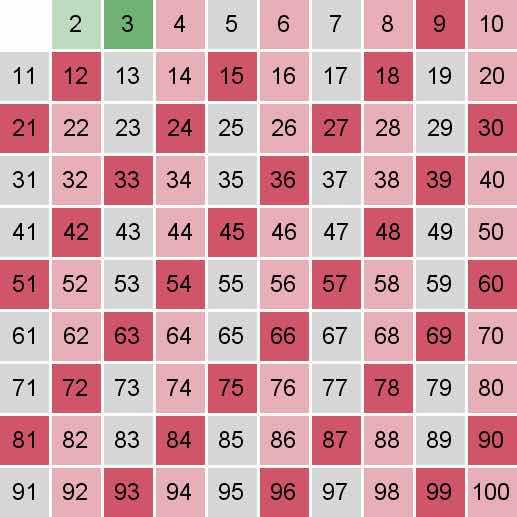
5是素数,标记所有5的倍数,从25开始
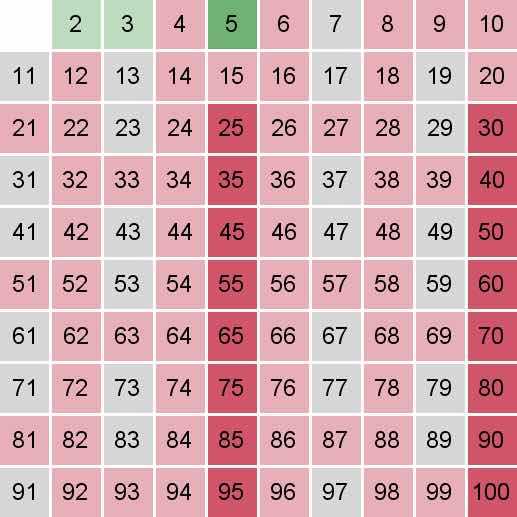
7是素数,标记所有7的倍数,从49开始
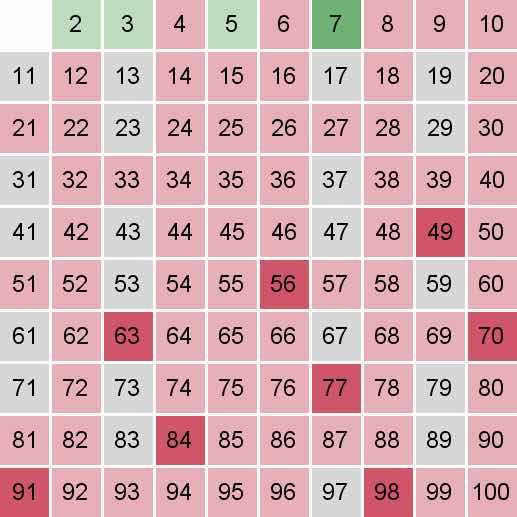
11的平方,超过了100,在数组里面所有没有被标记的数字都是素数
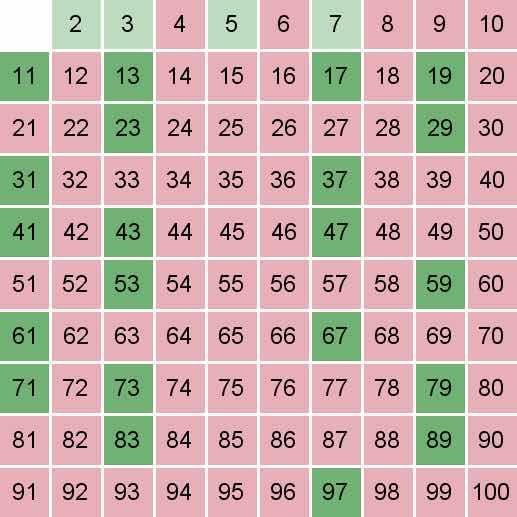
最终得到的结果
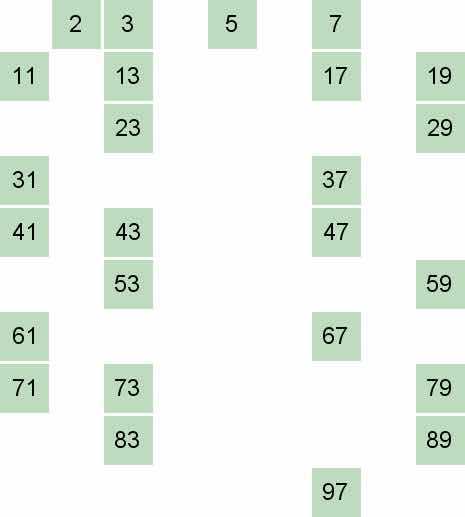
java代码(找出自然数upperBound内,包括upperBound的所有的素数,并且把它们输出)
1 public void runEratosthenesSieve(int upperBound) {
2 int upperBoundSquareRoot = (int) Math.sqrt(upperBound);
3 /*这里取平方是因为通过数学推理可以知道只需要判断到upperBound的上界即可。
4 第一次写的读者可以把循环的次数设置成upperBound,便于理解*/
5 boolean[] isComposite = new boolean[upperBound + 1];
6 //这个boolean类型的数组是为了标记upperBound以内的自然数
7
8 for (int m = 2; m <= upperBoundSquareRoot; m++) {
9 if (!isComposite[m]) {
10 System.out.print(m + " ");
11 for (int k = m * m; k <= upperBound; k += m)
12 isComposite[k] = true;
13 }
14 }
15 for (int m = upperBoundSquareRoot; m <= upperBound; m++)
16 if (!isComposite[m])
17 System.out.print(m + " ");
18 }
参考文献:
1.Peter J. Giblin. Primes and Programming.
2.Hans Riesel. Prime Numbers and Computer Methods for Factorization.
原文:https://www.cnblogs.com/HelloTum/p/9025584.html