好久没有更新专栏了,最近因为项目的原因接触到了PyTorch,感觉打开了深度学习新世界的大门.闲暇之余就用PyTorch训练了最近在图像分类上state-of-the-art的CNN模型,正好在文章中总结如下:
本文复现了上述论文在CIFAR数据集(包括cifaro10和cifar100)上的结果([9]除外),代码已经放在github上了:
这篇主要介绍前四个结构.
ResNet是近年来CNN结构发展中最为关键的一个结构,后面非常多的insight都是在resnet基础上进行改进,也有非常多的论文旨在分析残差结构的有效性.ResNet的成功首先得益于其结构的简单有效,其次得益于它的广泛适用.一个简单的残差块如下图所示:
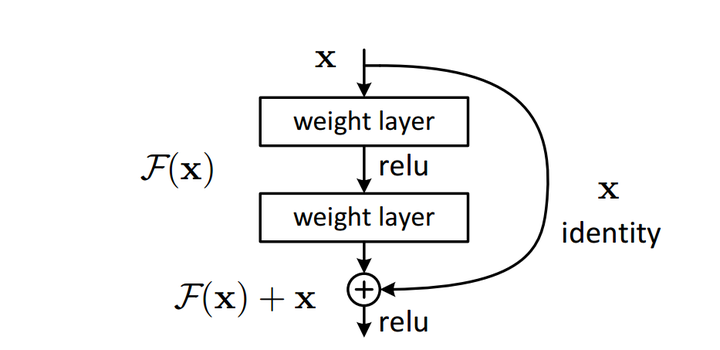 残差结构块
残差结构块
这个单元用可以由以下公式来表述:
在resnet的大多数结构块中, 亦即恒等映射,只有非常少的几个需要进行维度匹配而使用了1x1的卷积层来增加维度,而f则是ReLU函数.
假设从上一层传来的loss为 ,利用反向传播规则,有:
注意到 这一项,它使得梯度在层层传播中不致产生弥散情况,这可以一定程度上解释残差学习的有效性.
通过复现[1]中ResNet在cifar10上的结果,得到下表:
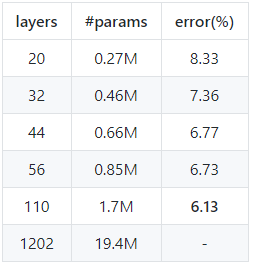 在cifar10上复现ResNet结果
在cifar10上复现ResNet结果
和原论文作对比,会发现复现结果均优于论文中的结果,1202层的网络也尝试跑了,可能由于没有按照原文中的学习率设置,导致结果一直不收敛,为节省GPU资源,就没有跑完最终结果,表明ResNet在极深情况下也会遇到优化问题,不过一般情况下也不会用到这么深的结构.
为解决上述问题,[2]中提出了PreAct的残差结构,如下图所示:
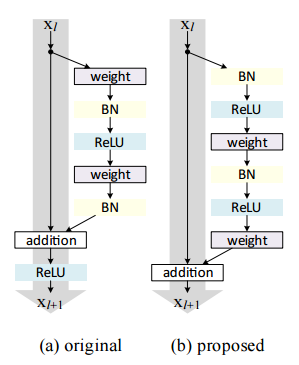 (a)普通的残差结构块,(b)PreAct残差结构块
(a)普通的残差结构块,(b)PreAct残差结构块
顾名思义,PreAct是指在卷积层之前使用BN和激活函数(ReLU),如上,我们给出这种结构的公式表示:
以上结构具有更加巧妙的形式,根据 ,递推地,则有:
对于任意地深层L和浅层l成立,
这个公式有一些很好的性质,
i).任意深层单元 可以用任意浅层单元
加上一个残差函数的和来表示;
ii). ,任意深层单元
是之前所有残差函数加和的结果(再加上
输入层)
假设loss函数是 ,根据反向传播,有:
如果我们忽略PreActResNet中的很少的用于增加维度的层,那么该公式表明:不管网络有多深,整个网络中的梯度流不会产生弥散问题.
下述实验结果也证明了这一点:
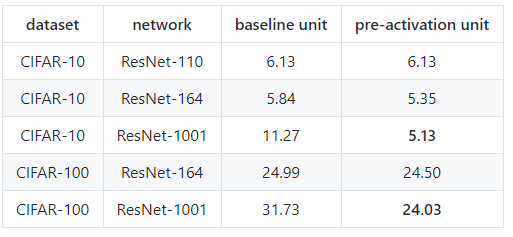 在cifar数据集上复现PreActResNet结果
在cifar数据集上复现PreActResNet结果
除了1001层的网络,上述结果均得到了比原论文中更好的结果,从该表中可以得出,
1.在网络极深情况下,PreAct单元比普通的残差单元要更加有效
2.即使是1000层的网络,使用同样的超参数设置,PreAct网络依然可以很好的收敛;
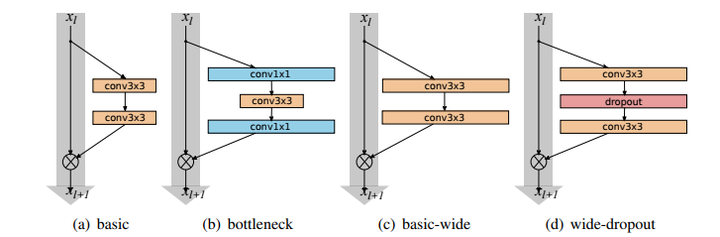 宽残差结构块
宽残差结构块
ResNet表明通过增加深度,网络可以得到更好的性能,而这一篇的insight则在于探究宽度对于网络性能的影响.首先我们说明一下什么是宽度.对于卷积层来说,宽度是指输出维度,如ResNet50的第一个卷积层参数为(64,3,7,7),宽度即输出维度也就是64.而对于一个网络来说,宽度则是指所有参数层的总体输出维度数.为了便于研究,通常通过一个倍率系数k来控制一个网络的宽度,如下表所示:
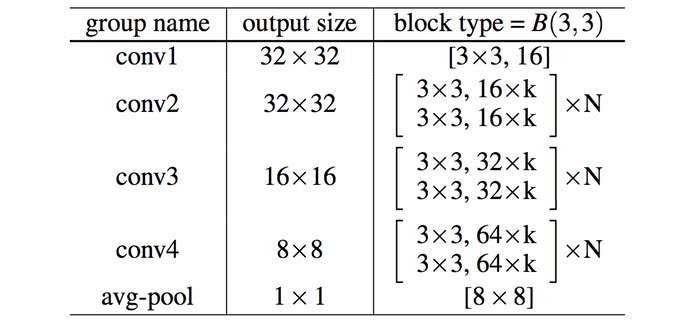 Wide ResNet在cifar数据集上的网络结构
Wide ResNet在cifar数据集上的网络结构
[3]的实验结果表明增加宽度,网络的性能也能得到提升.甚至一个14层深的宽残差网络可以达到比1001层深的残差网络更好的性能.同时,由于GPU的并行运算特性,在参数数量级一致的情况下,WRN(wide resnet缩写)的训练效率要远远高于ResNet.复现结果如下:
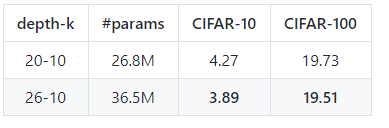 在cifar数据集上复现Wide ResNet实验结果
在cifar数据集上复现Wide ResNet实验结果
复现结果均优于论文中结果.
ResNeXt是Kaiming组的大作.[4]中提出除了深度和宽度以外,"基数"也是影响网络性能的一个重要因素.基数是什么呢?如下图所示
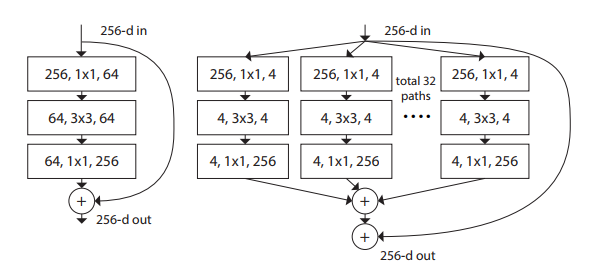 左:一个残差结构块,右:一个ResNeXt结构块(基数=32),每一层用#输入维数,过滤器尺寸,#输出维数表示
左:一个残差结构块,右:一个ResNeXt结构块(基数=32),每一层用#输入维数,过滤器尺寸,#输出维数表示
ResNeXt其实是一种多分支的卷积神经网络.多分支网络最初可见于Google的Inception结构.
基数在论文中的定义是转换集的尺寸.这个定义可能还不是很好理解,我们先来了解一下组卷积(group convolution).
组卷积可以最早可以追溯到AlexNet[6].Krizhevsky等人使用组卷积的目的是为了将模型分布到两个GPU上进行训练.在AlexNet中,group size为2,最近的很多篇论文,包括Xception[7],MobileNet以及这篇ResNeXt,都是组卷积的应用.Xception的group size为输入维数,这种组卷积也被称为depthwise卷积.Xception和MobileNet均使用了深度可分离卷积,所谓深度可分离卷积,其实就是depthwise卷积加上pointwise卷积(也就是卷积核尺寸为1x1的卷积)
了解完组卷积之后,我们再来看一下ResNeXt中基数的概念.可以发现,基数其实就是组卷积中的group size,也就是组数.depthwise卷积其实是ResNeXt的一种特例.
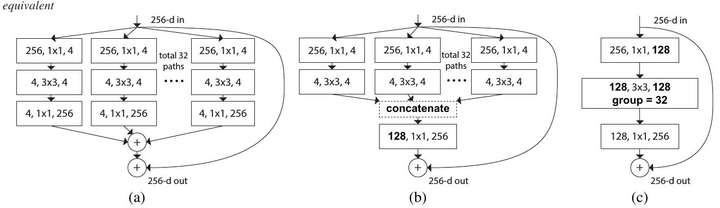 ResNeXt的三种等价形式
ResNeXt的三种等价形式
原文中,作者实现了所有这三种架构,并验证了它们的等价性.所以在复现过程中,我们只复现架构C,因为通过使用组卷积,这种架构最易于实现.复现结果如下:
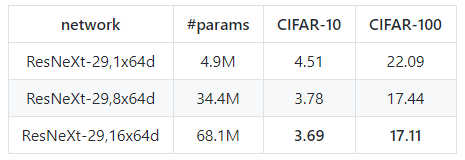 在cifar数据集上复现ResNeXt实验结果
在cifar数据集上复现ResNeXt实验结果
在cifar10上的结果稍差于论文中结果,在cifar100上的结果均优于论文中结果,并得到了目前最低的错误率(17.11%)
DenseNet是CVPR 2017年的best paper.虽然DenseNet的影响不及ResNet那么大,但是也提出了一种很有意义的insight. DenseNet的最大优势在于优化梯度流.早在ResNet之后,[8]就指出在ResNet训练过程中,梯度的主要来源是shortcut分支(这也侧面验证了我们之前关于残差结构块梯度传播的推导).大家都知道在BP过程中保持梯度流的有效性,防止梯度爆炸/消失在训练CNN时有多么重要,既然shortcut如此有效,那么为什么不多加点呢?这就是 DenseNet 的核心思想:对之前每一层都加一个单独的 shortcut,使得任意两层之间都可以直接"沟通".也就是如下图所示的结构:
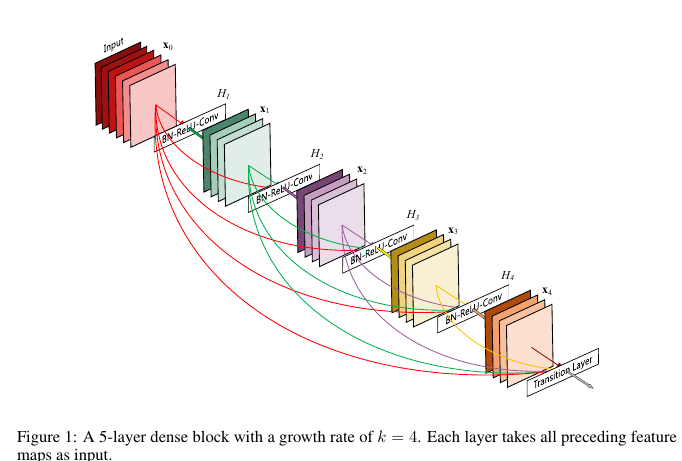
在具体实现过程中,是使用channel wide的concat操作实现任意两层之间互联的.
DenseNet的总体结构如下图所示:

具体的超参数设置可以参考论文和代码实现,复现结果如下:
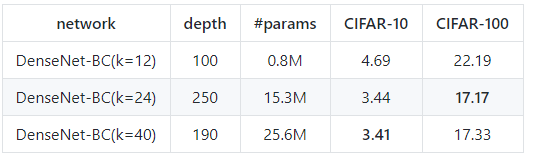 在cifar数据集上复现DenseNet实验结果
在cifar数据集上复现DenseNet实验结果
复现结果基本达到(或超过)论文中的结果.最后的结果基本达到了现在cifar数据集上的state-of-the-art.
个人感觉DenseNet之所以不那么火,是因为在ImageNet数据集上的效果不是非常好,相比于其他同等参数数量级的模型,如ResNeXt,SENet.
从ResNet到WRN再到ResNeXt,分别验证了深度,宽度,基数对于CNN模型的重要影响.从ResNet到PreActResNet再到DenseNet,通过对梯度流的不断优化,得到了越来越好的效果.
本文在PyTorch上复现了上述4篇论文在cifar数据集上的实验结果,得到了和原文一致甚至更好的结果,在cifar10上得到了3.41%的错误率,cifar100上得到了17.11%的错误率
[1] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016.
[2] K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings in deep residual networks. In ECCV, 2016.
[3] S. Zagoruyko and N. Komodakis. Wide residual networks. In BMVC, 2016.
[4] S. Xie, G. Ross, P. Dollar, Z. Tu and K. He Aggregated residual transformations for deep neural networks. In CVPR, 2017
[5] H. Gao, Z. Liu, L. Maaten and K. Weinberger. Densely connected convolutional networks. In CVPR, 2017
[6] K. Alex, I. Sutskever, and G. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012
[7] C. Fran?ois. Xception: Deep Learning with Depthwise Separable Convolutions. In arxiv, 2016
[8] V. Andreas, M. Wilber, and S. Belongie. Residual networks behave like ensembles of relatively shallow networks. In NIPS, 2016
[9] Y. Chen, J. Li, H. Xiao, X. Jin, S. Yan, J. Feng. Dual path networks. In NIPS, 2017
[10] B. Zoph, V. Vasudevan, J. Shlens, Q. Le. Learning transferable architectures for scalable image recognition. In arxiv, 2017
[11] J. Hu, L. Shen, G. Sun. Squeeze-and-excitation networks. In arxiv, 2017
[12] S. Sabour, N. Frosst, G. Hinton. Dynamic routing between capsules. In NIPS, 2017
原文:https://www.cnblogs.com/bonelee/p/9029934.html