也称电子签名,是指附加在某一电子文档中的一组特定的符号或代码,它是利用数学方法和密码算法对该电子文档进行关键信息提取并进行加密而形成的,用于标识签发者的身份以及签发者对电子文档的认可,并能被接受者用来验证该电子文档在传输过程中是否被篡改或伪造。

消息认证是指通过对消息或者消息有关的信息进行加密或签名变换进行的认证,目的是为了防止传输和存储的消息被有意无意的篡改,包括消息内容认证(即消息完整性认证)、消息的源和宿认证(即身份认证0)、及消息的序号和操作时间认证等。它在票据防伪中具有重要应用(如税务的金税系统和银行的支付密码器)。
消息认证所用的摘要算法与一般的对称或非对称加密算法不同,它并不用于防止信息被窃取,而是用于证明原文的完整性和准确性,也就是说,消息认证主要用于防止信息被篡改。
验证信息的来源是真是的,而不是伪造的,此为消息源认证;验证消息的完整性,即验证信息在传送或存储过程中是否被篡改。
·口令的安全性
·文件的完整性(譬如可信计算、文件病毒的检验、网页防篡改、黑白名单等应用。)
·密码协议的应用(譬如零知识证明、比特承诺、投掷硬币、电子商务的安全协议的许多应用。)
纯认证系统模型:
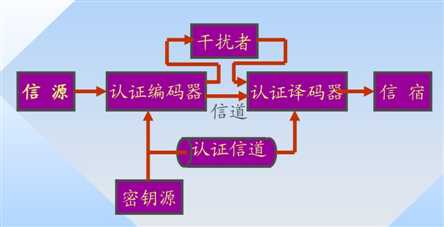
参考资料:
生日攻击:
利用“两个集合相交”问题的原理生成散列函数碰撞,达到目的的攻击称为生日攻击,也称为平方根攻击。 生日攻击方法没有利用Hash函数的结构和任何代数弱性质,它只依赖于消息摘要的长度,即Hash值的长度。
防范方法:
1.使用安全的Hash算法:安全的Hash算法生成的Hash值有足够多的位数。这样,攻击者在寻找两个具有相同Hash值的文件时就会非常困难。
2.加盐:在为文件签名之前,先向文件添加一个随机值,然后计算Hash值,再将文件、签名和随机值一起发送给接收者。这样,攻击者必须找出具有特定Hash值的伪造文件,这非常困难。
3.改动文件:在为文件签名之前,对消息或文件做少许改动。这样,攻击者必须找出具有特定Hash值的伪造文件,这非常困难。
MD5:
MD5即Message-Digest Algorithm 5(信息-摘要算法5),用于确保信息传输完整一致。是计算机广泛使用的杂凑算法之一(又译摘要算法、哈希算法),主流编程语言普遍已有MD5实现。将数据(如汉字)运算为另一固定长度值,是杂凑算法的基础原理,MD5的前身有MD2、MD3和MD4。
MD5算法具有以下特点:
1、压缩性:任意长度的数据,算出的MD5值长度都是固定的。
2、容易计算:从原数据计算出MD5值很容易。
3、抗修改性:对原数据进行任何改动,哪怕只修改1个字节,所得到的MD5值都有很大区别。
4、强抗碰撞:已知原数据和其MD5值,想找到一个具有相同MD5值的数据(即伪造数据)是非常困难的。
MD5的破解:
2004年8月17日的美国加州圣巴巴拉的国际密码学会议(Crypto’2004)上,来自中国山东大学的王小云教授做了破译MD5、HAVAL-128、 MD4和RIPEMD算法的报告,公布了MD系列算法的破解结果。宣告了固若金汤的世界通行密码标准MD5的堡垒轰然倒塌,引发了密码学界的轩然大波。(注意:并非是真正的破解,只是加速了杂凑冲撞)
2009年,冯登国、谢涛二人利用差分攻击,将MD5的碰撞算法复杂度从王小云的2^42进一步降低到2^21,极端情况下甚至可以降低至2^10。仅仅2^21的复杂度意味着即便是在2008年的计算机上,也只要几秒便可以找到一对碰撞。
SHA-1:
SHA-1是1995年国家标准技术局NIST(National Institute of Standards and Technology)于1995年标准化的哈希函数。与前身MD5相比,SHA-1的输出长度更长(MD5输出长度为128bit,而SHA-1的输出长度为160bit),这也意味着出现哈希碰撞的概率更低。同时,SHA-1的安全性似乎也比MD5更好。这里要稍微介绍一下寻找哈希函数碰撞的难度和一般方法了。以SHA-1为例,其哈希结果长度为160bit。如果SHA-1本身没有漏洞,而攻击者想找到一组碰撞的话,最显然的方法是选取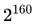 组不同的数据,依次计算它们的哈希结果。根据著名的抽屉原理,必然会出现一组数据,使得其哈希结果相同。此攻击方法需要调用
组不同的数据,依次计算它们的哈希结果。根据著名的抽屉原理,必然会出现一组数据,使得其哈希结果相同。此攻击方法需要调用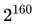 次SHA-1,即计算量级大约为
次SHA-1,即计算量级大约为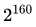 。
。
SHA-1的攻破:
2017年2月23日,荷兰阿姆斯特丹 Centrum Wiskunde & Informatica (CWI) 研究所和 Google 公司的研究人员 [Marc Stevens (CWI Amsterdam), Elie Bursztein (Google), Pierre Karpman (CWI Amsterdam), Ange Albertini (Google), Yarik Markov (Google), Alex Petit Bianco (Google), Clement Baisse (Google)] 在谷歌安全博客上发布了世界上第一例公开的 SHA-1 哈希碰撞实例!在经过两年的联合研究和花费了巨大的计算机时间之后,研究人员在他们的研究网站 SHAttered 上给出了两个内容不同,但是具有相同 SHA-1 消息摘要的 PDF 文件(PDF 1、 PDF 2),这就意味着在理论研究长期以来警示 SHA-1 算法存在风险之后,SHA-1 算法的实际攻击案例也浮出水面,同时也标志着 SHA-1 算法终于走向了生命的末期。
图中两个不同的PDF文件,但SHA-1消息摘要相同,SHA-256消息摘要不同:

散列函数的安全性:
安全散列函数结构:
因为所需的安全散列长度越来越长,因此我们可以使用有限定义域上的散列函数(俗称压缩函数)通过迭代方式拓展为具有无限定义域的散列函数。而最为代表性的就Merkle-Damgard结构。
Merkle-Damgard结构:
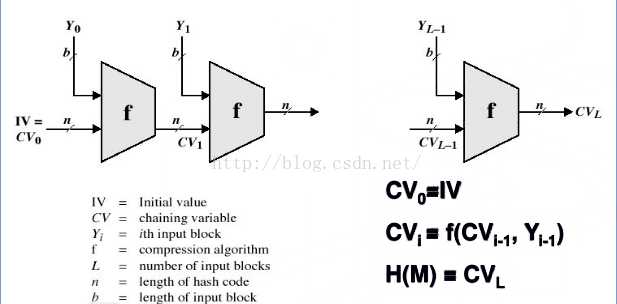
参考资料:
3.如何评价 2 月 23 日谷歌宣布实现了 SHA-1 碰撞? - 知乎
4.抗碰撞性、生日攻击及安全散列函数结构解析 - CSDN博客
前缀碰撞攻击:
对于MD5/SHA1更复杂的攻击目前主要有共同前缀碰撞攻击(Identical PrefixCollision)和选择前缀碰撞攻击(Chosen Prefix Collision)。共同前缀攻击是构造两个不同的消息s1和s2,他们由相同的前缀,和不同的尾部“碰撞块”组成。震惊世界的SHAttered攻击是对SHA1进行的共同前缀攻击。选择前缀攻击则是构造两个不同的消息s1和s2,他们不必有共同的前缀,但是经过在尾部附加不同的“碰撞块”后,两个消息的散列值相同。选择前缀攻击是包括共同前缀攻击的,因此共同前缀的攻击代价小于选择前缀攻击。在Marc Stevens(SHAttered作者)2009年的文章中对此类攻击的计算代价总结如表1。

表1:MD5和SHA1的两种不同攻击的计算代价
这里的单位是需要计算的hash的次数。例如2004年之前,对MD5的平凡攻击(生日攻击)需要蛮力计算2的64次方次md5 hash。在2009年时,对于MD5的共同前缀攻击计算代价是2的16次方次MD5 hash,对SHA1的则是2的52次方。不难看出,无论是共同前缀攻击,还是选择前缀攻击,都可以被应用在同谋碰撞攻击中。由于共同前缀攻击和选择前缀攻击的研究进展迅速,同谋碰撞攻击逐渐成为数字签名体系最大的威胁。
计算复杂度和最后构造出的碰撞结构有很大关系。对于共同前缀碰撞攻击,由王小云教授提出的攻击方法需要构造两个碰撞块,第一个碰撞块由生日攻击得到,目的是使得计算完第一碰撞块后的hash内部状态的差分满足特定形式。第二个碰撞块则由对差分路径的搜索得到。因此构造共同前缀碰撞攻击只需要两个碰撞块。对于选择前缀碰撞攻击,需要构造多个(>=2个)碰撞块。第一个碰撞块的作用相同,后续的碰撞块则对第一个碰撞块计算完成之后内部状态的区别做逐一修正。在唯一一份公开的选择前缀碰撞代码中,这个后续碰撞块的长度指定为9,意为需要构造9次修正块,以完成一次碰撞攻击。长度越短,对于每个碰撞块的要求就越高,计算所需的时间也指数级提高。在长度为9时,计算可以在普通计算机上运算几小时即可完成。
对于MD5碰撞的研究主要关注与快速发现MD5碰撞。王小云教授的著名工作等,以及谢涛的后续工作等,使得在短时间内构造简短的MD5碰撞成为可能。对SHA1最著名的攻击是最近的SHA1 Shattered攻击,是一种共同前缀碰撞攻击 。另一方面,利用选择前缀攻击,可以伪造X509格式的CA证书 ,以及构造多个消息的碰撞“Herding Attack”,可以用于“预测”任何一次的美国总统大选结果。 此外,对于攻击签名机制,还有一些由于签名机制实现不当而产生的漏洞和对应的攻击方法。下面我们简要介绍一下选择前缀碰撞攻击的能力,然后再讨论如何利用择前缀碰撞攻击,最后回顾一下对于基于hash的签名机制实现不当而产生的攻击。
两个可执行文件的摘要值:
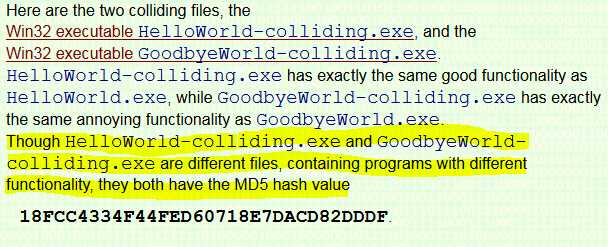
由图中黄色标识出的文字可知,虽然两个文件是不同的,但是他们的MD5码是相同的。
MD5算法来验证软件完整性时可能出现的问题:
经过对以上相关知识的了解,我认为在MD5算法在很短的时间就可以被攻破的情况下,再继续使用MD5算法来验证软件完整性的话就让人感觉不可靠。因为存在两个功能完全不同的软件但它们的MD5码确完全相同的情况,这种情况的存在使我们有理由怀疑即使在MD5校验成功,软件未被篡改的情况下,该软件的内容还是有可能已经被人所篡改,变成了一个完全不同的软件或是软件内部被人植入病毒等,则MD5的校验结果就变得不可信。
参考资料:
2.Software Integrity Checksum and Code Signing Vulnerability
原文:https://www.cnblogs.com/ForeverSevrous/p/9009189.html