归并排序(Merge Sort),又称二路归并排序,是指将一个数组一分为二,对每一个子数组递归排序,最后将排好的子数组合并为一个有序数组的过程。归并排序,是“分治法”应用的完美实现。

From Wikipedia:https://en.wikipedia.org/wiki/Merge_sort
1. 归并排序图示
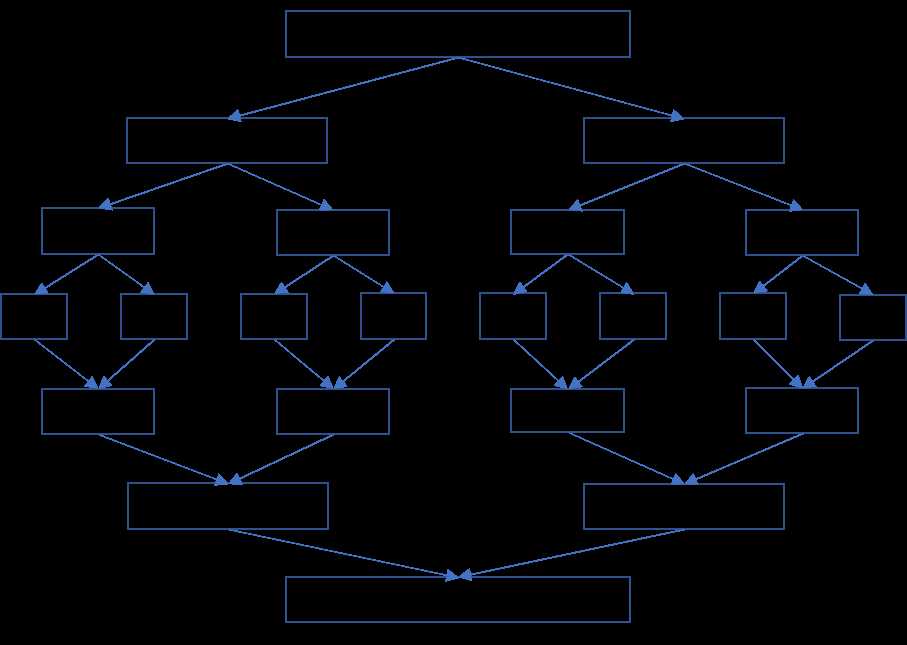
2. 归并排序流程
通过图示,可以发现归并排序一共只需要两个步骤:
3. 代码实现
对于归并排序来说,“分”这个步骤并没有什么特殊之处,但是“合”这一方面却可以做一些文章:
public abstract class BasicMergeSort implements Sort {
@Override
public void sort(int[] array) {
sort(array, 0, array.length - 1);
}
private void sort(int[] array, int left, int right) {
if (left < right) {
int mid = (left + right) >>> 1;
sort(array, left, mid);
sort(array, mid + 1, right);
merge(array, left, mid, right);
}
}
protected abstract void merge(int[] array, int left, int mid, int right);
}
3.1 开辟额外的数组空间
合并两个有序数组(长度分别为 n 和 m),可以开辟一个长度为 m+n 的新数组,,可以在线性的时间内完成合并工作。
public final class MergeSort1 extends BasicMergeSort {
@Override
protected void merge(int[] array, int left, int mid, int right) {
int[] newArray = new int[right - left + 1];
int startIndex1 = left;
int startIndex2 = mid + 1;
for (int i = 0; i < newArray.length; ++i) {
if (startIndex1 == mid + 1) {
newArray[i] = array[startIndex2++];
} else if (startIndex2 == right + 1) {
newArray[i] = array[startIndex1++];
} else {
newArray[i] = array[startIndex1] < array[startIndex2] ? array[startIndex1++] : array[startIndex2++];
}
}
System.arraycopy(newArray, 0, array, left, newArray.length);
}
}
3.2 使用直接插入排序
由于需要合并的数组,在原数组中是相邻的两部分,且前半部分已经有序,所以可以使用直接插入排序,在不使用额外空间的前提下完成合并。
public final class MergeSort2 extends BasicMergeSort {
@Override
protected void merge(int[] array, int left, int mid, int right) {
for (int i = mid + 1; i <= right; ++i) {
int cur = array[i];
boolean flag = false;
for (int j = i - 1; j >= left; --j) {
if (cur < array[j]) {
array[j + 1] = array[j];
} else {
array[j + 1] = cur;
flag = true;
break;
}
}
if (!flag) {
array[left] = cur;
}
}
}
}
通常意义上,归并排序,采取的是第一种做法。
4. 归并排序的时间复杂度和空间复杂度
4.1 使用额外空间
显而易见,递归的次数为 m = log2n,合并操作的时间消耗是线性的,所以时间复杂度 T(n) 如下:
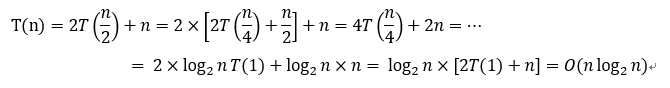
时间复杂度为O(n).
4.2 使用直接插入排序
空间复杂度 T(n) = O(n^2),时间复杂度为O(1)。
5. 归并排序的性能分析及优化
两种归并排序的算法,分别是采取了空间换时间,及时间换空间的策略,其性能各有优劣,但是通过分析可以得出以下特点:
根据以上两个性质,可以在归并排序中,设置一个阈值。
超过这个给定的阈值,则采取空间换时间的策略;反之,采用时间换空间的策略,从而提高归并排序的效率。
public class MixedMergeSort implements Sort {
private int threshold = 2 << 4;
private BasicMergeSort sort1 = new MergeSort1();
private BasicMergeSort sort2 = new MergeSort2();
public int getThreshold() {
return threshold;
}
public void setThreshold(int threshold) {
this.threshold = threshold;
}
@Override
public void sort(int[] array) {
sort(array, 0, array.length - 1);
}
private void sort(int[] array, int left, int right) {
if (left < right) {
int mid = (left + right) >>> 1;
sort(array, left, mid);
sort(array, mid + 1, right);
if (right - left > threshold) {
sort1.merge(array, left, mid, right);
} else {
sort2.merge(array, left, mid, right);
}
}
}
}
Source Code: https://github.com/Gerrard-Feng/algorithm-learning.git
原文:https://www.cnblogs.com/jing-an-feng-shao/p/9038915.html