BZOJ 1005 明明的烦恼 (组合数学）

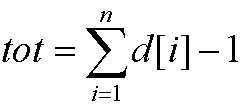
题解：n为树的节点数，d[ ]为各节点的度数，m为无限制度数的节点数。

则            

所以要求在n-2大小的数组中插入tot各序号，共有种插法；

在tot各序号排列中，插第一个节点的方法有种插法；

插第二个节点的方法有种插法；

                                      .........

另外还有m各节点无度数限制，所以它们可任意排列在剩余的n-2-tot的空间中，排列方法总数为

根据乘法原理：

            

#include <cstdio>
#include <cmath>
int n,m,tot,i,j,d,down[1005],up[1005],p[1005],ans[10005];
void pi(int x,int a[]){
    for(int i=2;i<=x;i++)if(p[i]){
        int sum=i; while(sum<=x)a[i]+=x/sum,sum*=i;
    }
}
int main(){
    scanf("%d",&n);
    for(i=2;i<=1000;i++){
        for(j=2;j<=std::sqrt(i);j++)
        if(i%j==0)break;
        if(j>sqrt(i))p[i]=1;
    }
    for(i=1;i<=n;i++){
        scanf("%d",&d);
        if(d==-1){m++;continue;}
        if(d>1)pi(d-1,down);
        tot+=d-1;
    }
    pi(n-2-tot,down);pi(n-2,up);
    for(i=1;i<=1000;i++)up[i]-=down[i];
    ans[0]=1;
    for(i=1;i<=1000;i++)while(up[i]--){
        for(j=0;j<=10000;j++)ans[j]*=i;
        for(j=0;j<=10000;j++)if(ans[j]>9)ans[j+1]+=ans[j]/10,ans[j]%=10;
    }
    if(m)for(i=1;i<=n-2-tot;i++){
        for(j=0;j<=10000;j++)ans[j]*=m;
        for(j=0;j<=10000;j++)if(ans[j]>9)ans[j+1]+=ans[j]/10,ans[j]%=10;
    }
    if(tot>n-2||tot<n-2&&m==0)return puts("0"),0; 
    i=10000; while(!ans[i])i--;
    while(~i)printf("%d",ans[i--]);
    return 0;
}

BZOJ 1005 明明的烦恼 (组合数学）,布布扣,bubuko.com

BZOJ 1005 明明的烦恼 (组合数学）

原文：http://www.cnblogs.com/forever97/p/bzoj1005.html