1970年由E.F.Codd提出,后又提出关系代数和演算
关系和关系模式往往统称为关系,通过上下文区别
一组具有相同数据类型的值的集合
1、给定域D1、D2、D3…Dn,允许某些域相同,笛卡尔积为:
D1*D2*D3…Dn={(d1,d2…dn)|di∈Di,i=1,2,3…n}
2、基数(cardinal number)
基数(数学):数学上一个集合的元素个数
则D1*D2*D3…Dn基数M
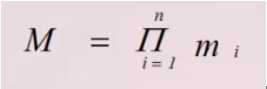
3、表示方式
一张二维表,每行为一个元组,每列为一个域

笛卡尔积的子集为关系,表示为:
R(D1,D2…Dn)
R:关系名
N:关系的目或度(Degree)
n元祖(n-tuple):简称元祖(t),是关系中的每一个元素(d1,d2,d3…dn)
不同列可以对应相同的域
属性(attribute):每列的名字
N目关系有n个属性
1)候选码(candidate key)
关系中某一属性组唯一标识一个元祖,则为候选码
2)全码(all-key)
关系模式的所有属性组为这个关系模式的候选码
3)主码(primary key)
一个关系有多个候选码,选择其中一个为主码
4)主属性(prime attribute)
候选码的属性
不包括在候选码的属性为非主属性(non-prime attribute)或者非码属性(non-key attribute)
5)单元关系与二元关系
n=1:单元关系或者一元关系(unary relation)
n=2:二元关系(binary relation)
6)基本关系的性质

分量必须取原子值
型,是对关系的描述
元祖集合的结构:1)属性构成 2)来自的域 3)与域的映像关系
完整性约束条件
R(U,D,DOM,F)

给定的应用领域,关系集合构成关系数据库
型:关系数据库模式
值:常称为关系数据库,关系模式在某一时刻对应的关系的集合
原文:https://www.cnblogs.com/thyHome/p/9094974.html