极大团。即求一个最大点集,使得点集中的任意两个点u,v至少存在u->v,或者v->u的路径。
是这样做的,求出所有的联通分量,然后整个图就变成了无环图,把原来若干个点缩点,点权为分量的点数。这样相当于找一条权值最大的路径,因为无环了,所以这个可以通过先拓扑排序然后dp解决。
这里重点说一下自己遇到的坑吧。
d[cur]=low[cur]=++dfsclock; 绝不能是 d[cur]=low[cur]=d[fa]+1;
后者是错的。
我思考了好久后来才发现问题。如图:
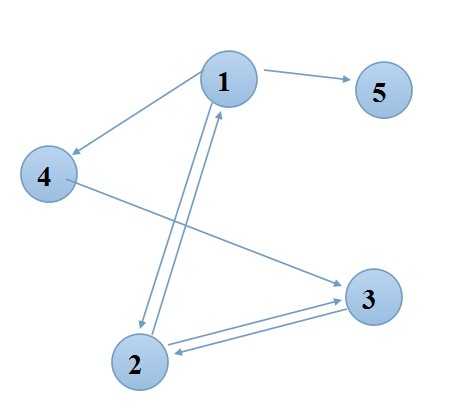
假设我们按照d[fa]+1的方法来打标记,那么当路径为1->2->3时候,递归返回的时候low[1]=1,low[2]=1,low[3]=2,而此时去访问4点,此时low[4]最少也只能是2,那么从程序的角度来说,也就认为了4是单独的强联通分量,这是不对的。
但是如果我们按照++dfsclock的方法来打标记,那么low[1]=1,low[2]=1,low[3]=2,low[4]=2,但是此时d[4]=4,可以判断出不是一个单独的强连通分量。主要是通过++dfsclock可以判断是否以前被访问过,这里与源点距离无关,特别注意了。
召唤代码君:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #define maxn 1010 #define maxm 202000 using namespace std; int first[maxn],next[maxm],to[maxm],edge; int low[maxn],d[maxn],belong[maxn],scc; int U[maxm],V[maxm],stack[maxn],top; int f[maxn],sum[maxn],Q[maxn]; int n,m,T,ans,dfsclock; bool cmp(int q1,int q2) { return d[q1]>d[q2]; } void _init() { dfsclock=ans=top=scc=0,edge=-1; for (int i=1; i<=n; i++) first[i]=-1,low[i]=d[i]=belong[i]=0; } void addedge(int uu,int vv) { edge++; to[edge]=vv,next[edge]=first[uu],first[uu]=edge; } void dfs(int cur,int fa) { d[cur]=low[cur]=++dfsclock; stack[++top]=cur; for (int i=first[cur]; i!=-1; i=next[i]) { if (belong[to[i]]) continue; if (!d[to[i]]) dfs(to[i],cur); low[cur]=min(low[cur],low[to[i]]); } if (low[cur]>=d[cur]) for (scc++,f[scc]=0;;) { belong[stack[top--]]=scc; f[scc]++; if (stack[top+1]==cur) break; } } int get(int x) { if (d[x]!=0) return d[x]; if (first[x]==-1) return d[x]=1; d[x]=0; for (int i=first[x]; i!=-1; i=next[i]) d[x]=max(d[x],get(to[i])+1); return d[x]; } int main() { scanf("%d",&T); while (T--) { scanf("%d%d",&n,&m); _init(); for (int i=1; i<=m; i++) { scanf("%d%d",&U[i],&V[i]); addedge(U[i],V[i]); } for (int i=1; i<=n; i++) if (!d[i]) dfs(i,0); edge=-1; for (int i=1; i<=scc; i++) first[i]=-1,d[i]=0; for (int i=1; i<=m; i++) if (belong[U[i]]!=belong[V[i]]) addedge(belong[U[i]],belong[V[i]]); for (int i=1; i<=scc; i++) { Q[i]=i,sum[i]=0; if (!d[i]) d[i]=get(i); } sort(Q+1,Q+1+scc,cmp); for (int i=1; i<=scc; i++) { sum[Q[i]]+=f[Q[i]]; ans=max(ans,sum[Q[i]]); for (int j=first[Q[i]]; j!=-1; j=next[j]) sum[to[j]]=max(sum[to[j]],sum[Q[i]]); } printf("%d\n",ans); } return 0; }
UVA11324_The Largest Clique,布布扣,bubuko.com
原文:http://www.cnblogs.com/Canon-CSU/p/3852465.html