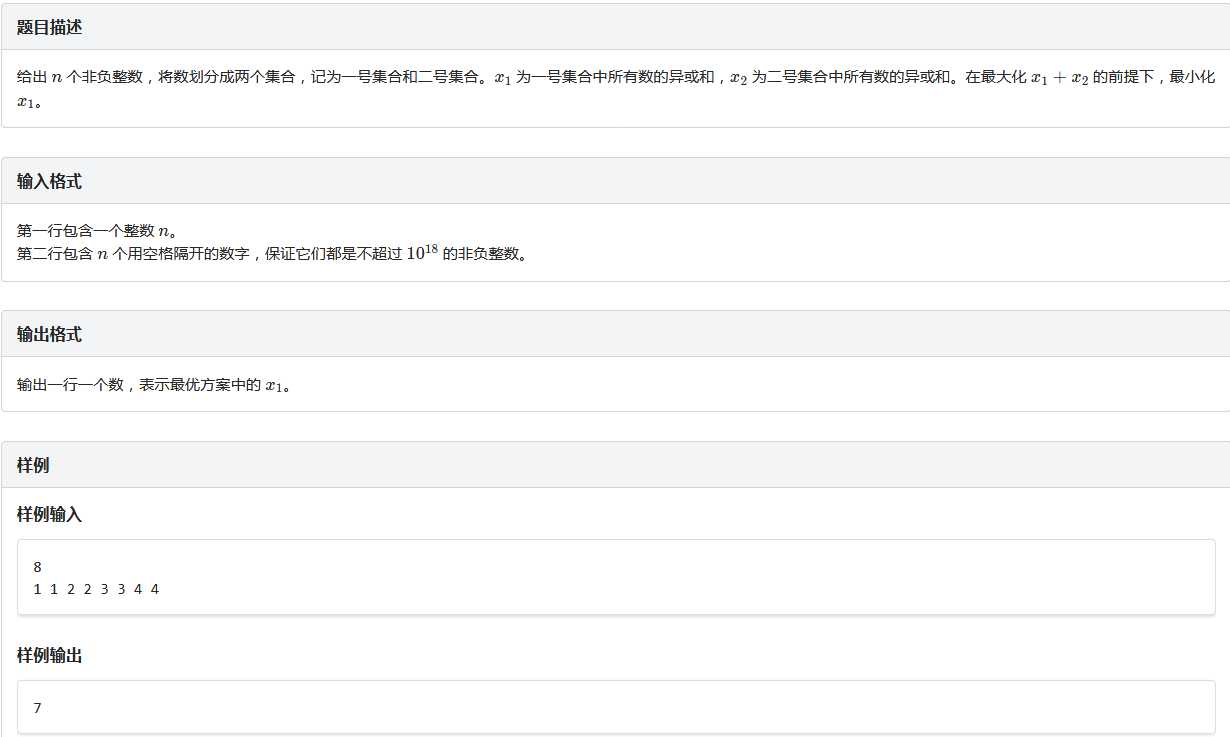
原题是CF上的某题,但是还要输出方案。。。。好鬼畜啊WWW
发现答案肯定是优先 xorsum^x1 + x1 最大,然后再优先x1最小(也就是 xorsum^x1 最大)。
我们把xorsum二进制分解一下,如果要让 xorsum^x1 + x1最大,那么肯定先得是 xorsum 为0的位 x1 在这一位是1再好不过了,并且是贪心的从高位到低位。。。
同样的,xorsum为1的位 xorsum^x1 在这里为1也再好不过了,同样是贪心的从高位到低位。。。。
这种贪心的思想实际上就已经把 二进制的每一位给排了一下优先级,先是 xorsum 为0的位 优先级要高于 xorsum 为1的位,然后再是高位优先于低位。。。。
然后这种任意子集的异或肯定是线性基没错啦。。。只不过传统的线性基是优先级只有高位到低位;所以这个题也得按照特殊的优先级插入。。。然后再按照特殊的优先级贪心就行了。。。。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=67;
ll ci[maxn],a[maxn],n;
ll Xor,now,num[100005];
inline void ins(ll x){
for(int i=60;i>=0;i--) if(!(Xor&ci[i])) if(x&ci[i]){
if(!a[i]){ a[i]=x; return;}
x^=a[i];
}
for(int i=60;i>=0;i--) if(Xor&ci[i]) if(x&ci[i]){
if(!a[i]){ a[i]=x; return;}
x^=a[i];
}
}
inline ll read(){
ll x=0; char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);ch=getchar()) x=x*10ll+ch-‘0‘;
return x;
}
inline void solve(){
now=0;
for(int i=60;i>=0;i--) if(!(Xor&ci[i])&&!(now&ci[i])) now^=a[i];
for(int i=60;i>=0;i--) if((Xor&ci[i])&&!(now&ci[i])) now^=a[i];
}
int main(){
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
ci[0]=1;
for(int i=1;i<=60;i++) ci[i]=ci[i-1]+ci[i-1];
scanf("%d",&n);
for(int i=1;i<=n;i++) num[i]=read(),Xor^=num[i];
for(int i=1;i<=n;i++) ins(num[i]);
solve();
printf("%lld\n",Xor^now);
return 0;
}
Loj #6060. 「2017 山东一轮集训 Day1 / SDWC2018 Day1」Set
原文:https://www.cnblogs.com/JYYHH/p/9102426.html