———其实这是很简单又很难得一些东西
树状图是一种数据结构,它是由\(n (n>=1)\)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
树(tree)是包含$ n(n>0)$个结点的有穷集,其中:
1)每个元素称为结点(node)
2)有一个特定的结点被称为根结点或树根(root)
3)除根结点之外的其余数据元素被分为\(m(m≥0)\)个互不相交的集合\(T_1,T_2,\cdots T_{m-1}\),其中每一个集合\(T_i(1<=i<=m)\)本身也是一棵树,被称作原树的子树(subtree)
树要满足一些特性:
1)树上两点间有且只有一条路径(不走重复路径)
2)每个节点有零个或多个子节点
3)没有父节点的节点称为根节点
4)每一个非根节点有且只有一个父节点
5)除了根节点外,每个子节点可以分为多个不相交的子树

1)节点的度:一个节点含有的子树的个数称为该节点的度;
2)叶节点或终端节点:度为0的节点称为叶节点;
3)非终端节点或分支节点:度不为0的节点;
4)双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
5)孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
6)兄弟节点:具有相同父节点的节点互称为兄弟节点;
7)树的度:一棵树中,最大的节点的度称为树的度;
8)节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
9)树的高度或深度:树中节点的最大层次;
10)堂兄弟节点:双亲在同一层的节点互为堂兄弟;
11)节点的祖先:从根到该节点所经分支上的所有节点;
12)子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
13)森林:由m(m>=0)棵互不相交的树的集合称为森林;
1)二叉树
2)线段树
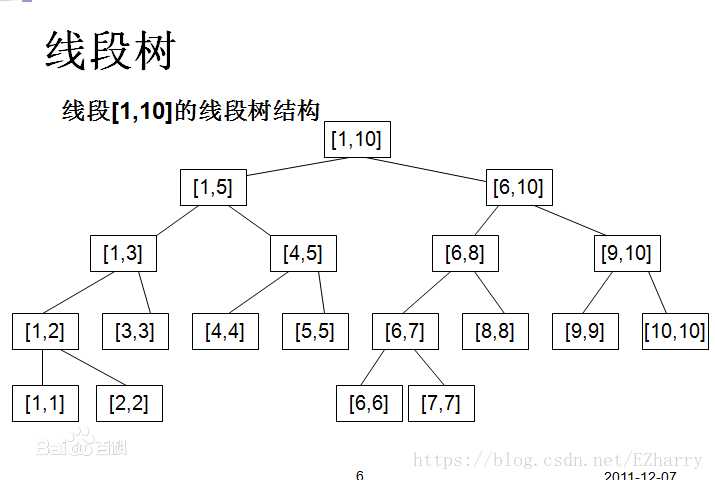
3)平衡树(如splay,treap,替罪羊树等)

4)trie字符树

5)……
传统“树论”:
1)各种维护数据结构,如[NOI2005]维护数列
2)树链剖分,如树链剖分
3)树上乱搞(LCA,dp,倍增等),如[LNOI2014]LCA
4)……
原文:https://www.cnblogs.com/ezoihy/p/9116282.html