图是由顶点集合V和边集合E组成的。分为有向图和无向图。
有向图的抽象数据类型定义
ADT Graph{
数据:
顶点的有限非空顶点集合V和边集合E,每条边由顶点的偶对<u,v>表示。数据元素之间的关系是多对多的关系。
运算:
Init(G,n):初始化运算。构造一个包含n个顶点没有边的图G。若构建成功,返回OK;否则,返回ERROR。
Destroy(G):撤销运算。撤销一个图G。
Exist(G,u,v):边的搜索运算。若图G中存在边<u,v>,则返回OK,否则返回Error。
Insert(G,u,v,w):边的插入运算。向图G中添加权为w的边<u,v>,若插入成功,返回OK;若图中已存在边<u,v>,则返回Duplicate;其他均返回ERROR。
Remove(G,u,v):边的删除运算。从图G中删除边<u,v>,若不存在则返回NotPresent;若存则则删除此边,返回OK;其他均返回Error。
}
如果u和v之间存在边,则在无向图或有向图对应的邻接矩阵中相应位置定义为1,否则定义为0。如果是带权图,则应标明权值,其他为∞。
#include <stdio.h> #define MaxVex 100 //最大顶点数 #define INFINITY 65535 //表示∞ #define TRUE 1 #define FALSE 0 typedef char VertexType; //顶点类型 typedef int EdgeType; //权值类型 typedef int Bool; Bool visited[MaxVex]; typedef struct { VertexType vexs[MaxVex]; //顶点数组 EdgeType arc[MaxVex][MaxVex]; //邻接矩阵 int numVertexes, numEdges; //当前图中的结点数以及边数 }MGraph; //广度优先遍历需要的循环队列 typedef struct { int data[MaxVex]; int front, rear; }Queue; /****************************************/ //队列的相关操作 //初始化 void InitQueue(Queue *Q) { Q->front = Q->rear = 0; } //入队 void EnQueue(Queue *Q, int e) { if ((Q->rear+1)%MaxVex == Q->front) return ; Q->data[Q->rear] = e; Q->rear = (Q->rear+1)%MaxVex; } //判空 Bool QueueEmpty(Queue *Q) { if (Q->front == Q->rear) return TRUE; else return FALSE; } //出队 void DeQueue(Queue *Q, int *e) { if (Q->front == Q->rear) return ; *e = Q->data[Q->front]; Q->front = (Q->front+1)%MaxVex; } /****************************************/ //建立图的邻接矩阵 void CreateMGraph(MGraph *G) { int i, j, k, w; printf("输入顶点数和边数: "); scanf("%d%d", &G->numVertexes,&G->numEdges); fflush(stdin); printf("==============================\n"); printf("输入各个顶点:\n"); for (i=0; i<G->numVertexes; ++i) { printf("顶点%d: ",i+1); scanf("%c", &G->vexs[i]); fflush(stdin); } for (i=0; i<G->numVertexes; ++i) { for (j=0; j<G->numVertexes; ++j) G->arc[i][j] = INFINITY; } printf("==============================\n"); for (k=0; k<G->numEdges; ++k) { printf("输入边(vi, vj)中的下标i和j和权W: "); scanf("%d%d%d", &i,&j,&w); G->arc[i][j] = w; G->arc[j][i] = G->arc[i][j]; } } //输出 void DisMGraph(MGraph *G) { int i, j, k; k = G->numVertexes; for (i=0; i<k; ++i) { for (j=0; j<k; ++j) { printf("%5d ", G->arc[i][j]); } putchar(‘\n‘); } } /****************************************/ //图的深度优先遍历 void DFS(MGraph G, int i) { int j; visited[i] = TRUE; printf("%c ", G.vexs[i]); for (j=0; j<G.numVertexes; ++j) { if (G.arc[i][j]!=INFINITY && !visited[j]) DFS(G, j); } } void DFSTraverse(MGraph G) { int i; for (i=0; i<G.numVertexes; ++i) visited[i] = FALSE; for (i=0; i<G.numVertexes; ++i) { if (!visited[i]) DFS(G, i); } } //图的广度优先遍历 void BFSTraverse(MGraph *G) { int i, j; Queue Q; for (i=0; i<G->numVertexes; ++i) visited[i] = FALSE; InitQueue(&Q); for (i=0; i<G->numVertexes; ++i) { if (!visited[i]) { visited[i] = TRUE; printf("%c ", G->vexs[i]); EnQueue(&Q, i); while (!QueueEmpty(&Q)) { DeQueue(&Q, &i); for (j=0; j<G->numVertexes; ++j) { if (!visited[j] && G->arc[i][j]!=INFINITY) { visited[j] = TRUE; printf("%c ", G->vexs[j]); EnQueue(&Q, j); } } } } } } /****************************************/ //程序入口 int main(){ MGraph G; CreateMGraph(&G); printf("\n图的深度优先遍历为: "); DFSTraverse(G); printf("\n图的广度优先遍历为: "); BFSTraverse(&G); printf("\n"); return 0; }
在邻接表中,为图的每个顶点建立一个单链表。单链表中的每个结点代表一条边,称为边结点。
使用一维指针数组存储每条单链表中第一个边结点的地址。
/** 无向图的邻接表存储 深度优先遍历递归 广度优先遍历递归+非递归 */ #include <stdio.h> #include <string.h> #include <malloc.h> #define N 5 #define MAX 50 typedef struct A{ int adjvex; struct A* nextArc; }Arc; typedef struct node{ char data[N]; Arc* firstArc; }Node; typedef struct graph{ Node vex[MAX]; int numv; int nume; }Graph; int getIndex(Graph G,char s[]){ for(int i = 0; i < G.numv; i++){ if(strcmp(G.vex[i].data,s) == 0) return i; } return -1; } void create(Graph& G){ printf("输入顶点和弧的个数:\n"); scanf("%d%d",&G.numv,&G.nume); printf("输入顶点信息:\n"); for(int i = 0; i < G.numv; i++) scanf("%s",G.vex[i].data); ///初始化顶点数组 for(int i = 0; i < G.numv; i++) G.vex[i].firstArc = NULL; printf("输入边的信息:\n"); char s[N],e[N]; int u,v; for(int i = 0; i < G.nume; i++){ scanf("%s%s",s,e); u = getIndex(G,s); v = getIndex(G,e); Arc* p = (Arc*)malloc(sizeof(Arc)); p->adjvex = v; p->nextArc = NULL; p->nextArc = G.vex[u].firstArc; G.vex[u].firstArc = p; Arc* t = (Arc*)malloc(sizeof(Arc)); t->nextArc = NULL; t->adjvex = u; t->nextArc = G.vex[v].firstArc; G.vex[v].firstArc = t; } } void output(Graph G){ Arc* p; for(int i = 0; i < G.numv; i++){ p = G.vex[i].firstArc; printf("%4s",G.vex[i].data); while(p != NULL){ printf("%4s",G.vex[p->adjvex].data); p = p->nextArc; } printf("\n"); } } ///深度优先遍历 (递归) int visit[2*MAX]; void dfs(Graph G,int s){ Arc* p = G.vex[s].firstArc; if(!visit[s]){ printf("%4s",G.vex[s].data); visit[s] = 1; } while(p != NULL){ if(!visit[p->adjvex]) dfs(G,p->adjvex); p = p->nextArc; } } ///广度优先遍历 (递归) ///缺点递归最大为G.numv次 int q[2*MAX],f=0,r=0; int visit_q[MAX]; void bfs(Graph G,int s){ if(!visit_q[s]){ printf("%4s",G.vex[s].data); visit_q[s] = 1; Arc* p = G.vex[s].firstArc; while(p != NULL){ if(!visit_q[p->adjvex]) q[r++] = p->adjvex; p = p->nextArc; } } while(f < r){ bfs(G,q[f++]); } } ///广度优先遍历 (非递归) int Q[2*MAX],F=0,R=0; int visit_Q[MAX]; void bfs_1(Graph G,int s){ printf("%4s",G.vex[s].data); visit_Q[s] = 1; Arc* p = G.vex[s].firstArc; while(p != NULL){ Q[R++] = p->adjvex; p = p->nextArc; } while(F < R){ int node = Q[F++]; if(!visit_Q[node]){ printf("%4s",G.vex[node].data); visit_Q[node] = 1; p = G.vex[node].firstArc; while(p != NULL){ if(!visit_Q[p->adjvex]) Q[R++] = p->adjvex; p = p->nextArc; } } } } int main(void){ Graph G; create(G); printf("输出邻接矩阵:\n output(G); printf("深度优先遍历(递归):\n"); dfs(G,0); printf("\n广度优先遍历(递归):\n"); bfs(G,0); printf("\n广度优先遍历(非递归):\n"); bfs_1(G,0); return 0; }
AOV网(顶点活动网):为反映整个工程之间的领先关系,使用一个有向图,顶点代表活动,图中的有向边代表活动间的领先关系。
排序步骤:
算法步骤:
对于有n个顶点和e条边,时间复杂度为O(n+e)。
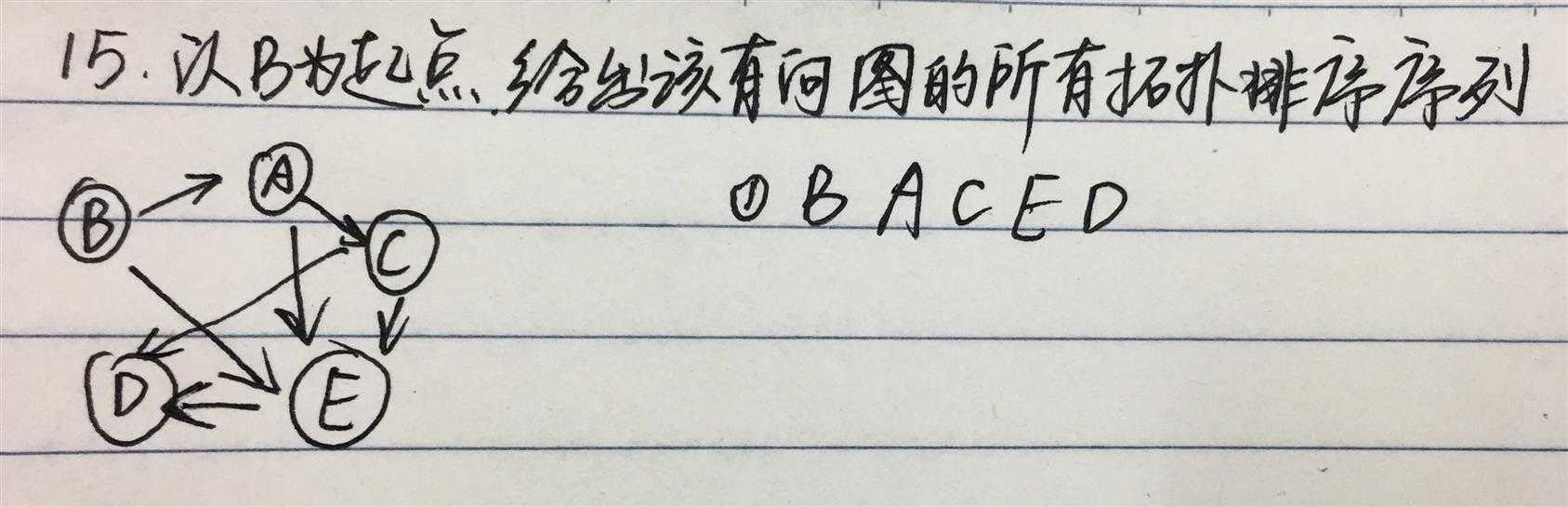
AOE网(活动边网络):AOE网是一个带权有向图,以顶点表示事件,有向边表示活动,边上权表示活动持续的时间。AOE网可以用来估算工程的完成时间。
解决估算问题的方法之一是关键路径算法。所谓关键路径,就是AOE网络中从开始顶点到完成顶点的最长路径。完成工程所需的最短时间是关键路径的长度,也就是关键路径上个边的权值和。关键路径上 的活动称为关键活动。
关键路径的求解步骤:
目标就是使用n-1条边将n个顶点连接起来,且各边的权值和最小。
最小生成树的构造过程是
代码:
时间复杂度为O(n2).
找道题目做做。
 、
、
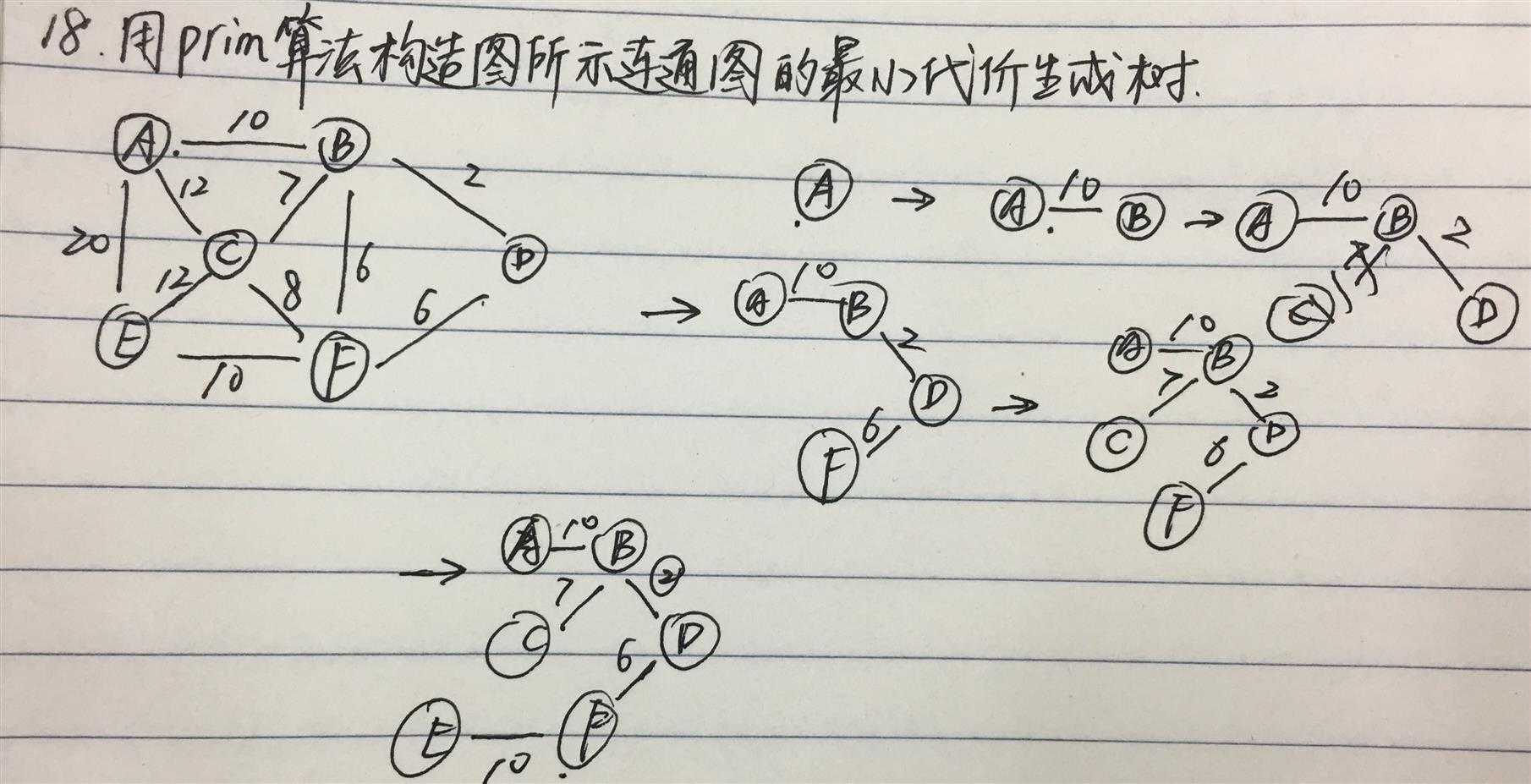
设G=(V,E)是带权连通图,T=(V‘,E‘)是正在构造中的生成树,最小代价生成树的构造过程是:
时间复杂度为O(elog2e)
算法思想:对于带权的有向图G=(V,E),将V中的顶点分为两个集合,集合S中存放已求出最短路径的顶点,集合V-S存放尚未确定最短路径的顶点。初始状态时,集合S中只有源点v0。按各顶点到源点最短路径长度非递减的顺序逐个将V-S中的顶点加到 S中,直到源点到其他顶点的最短路径均求得为止。
借鉴http://www.360doc.cn/article/27915668_540045384.html
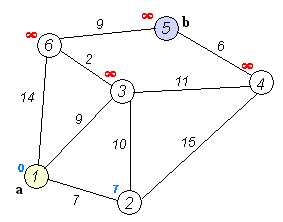
步骤如下:
同上,以6为前驱节点,得到4和5的计算距离为[20, 20],与上一轮进行比较,刷新后为[20, 20],二者相等只剩下两个节点,并且二者想等,剩下的计算已经不需要了。则两个节点的最短路径都为20。整个计算结束。4的最短路径为20,路线:1->3->4。5的最短路径为20,路线:1->3->6->5。
如果二者不相等,则还需要进行第五轮,先确定二者中的一个的最短路径和路线,再取定剩下的。直到整个5次循环都完成。
算法的时间复杂度应该是O(n3)
我做道题试验试验。
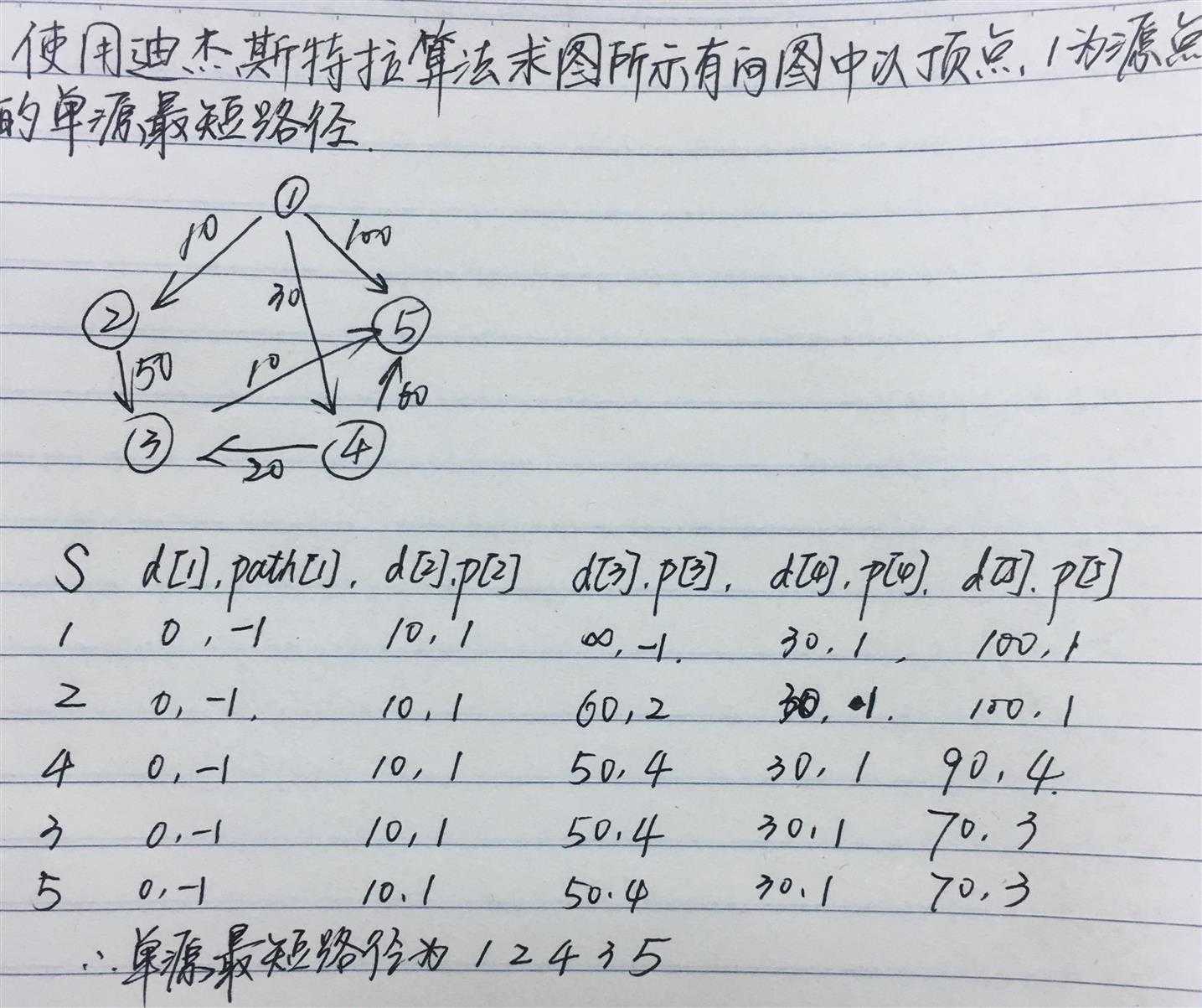
基本思想是:递推产生n*n的矩阵序列,其中dk [i][j]表示从顶点i到顶点j的路径上所经过的顶点序号不大于k的最短路径长度。
算法的时间复杂度应该是O(n3)
借鉴https://blog.csdn.net/luo_xianming/article/details/44998227
原文:https://www.cnblogs.com/WittPeng/p/9133667.html