三角形求交算法

在光线追踪中，我们常常要处理对于Mesh的渲染，由于Mesh一般由一个个三角形所构成，因此需要我们去计算光线和Mesh每个三角形之间是否存在交点。这可以看做是一个射线和三角形的求交问题。《Fundamentals of Computer Graphics (3rd edition)》中提出了一个in-place的算法，在这里予以介绍。

设光线的起点为e，方向为d，三角形三个顶点为a,b,c。那么可以得到：

e+td=a+β(b-a)+γ(c-a)

其中，β、γ为三角形的重心坐标。β+γ<1。那么可以得到以下公式：

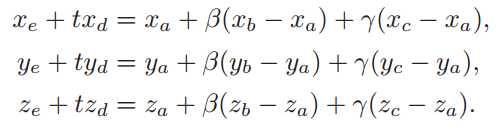
将它化为线性方程组：

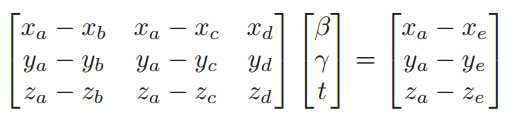
那么我们要求解的其实就是β、γ和t，接下来利用Cramer法则求解即可。

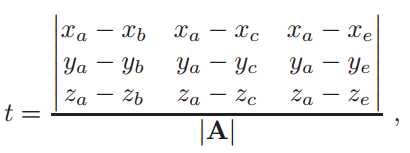
其中矩阵A为：

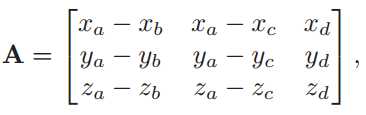
当|A|为0，或β+γ>1时，说明光线和该三角形不想交，否则可计算出交点p=e+td

三角形求交算法

原文：https://www.cnblogs.com/wickedpriest/p/9193314.html