1.学习总结(2分)

1.1图的思维导图

1.2 图结构学习体会

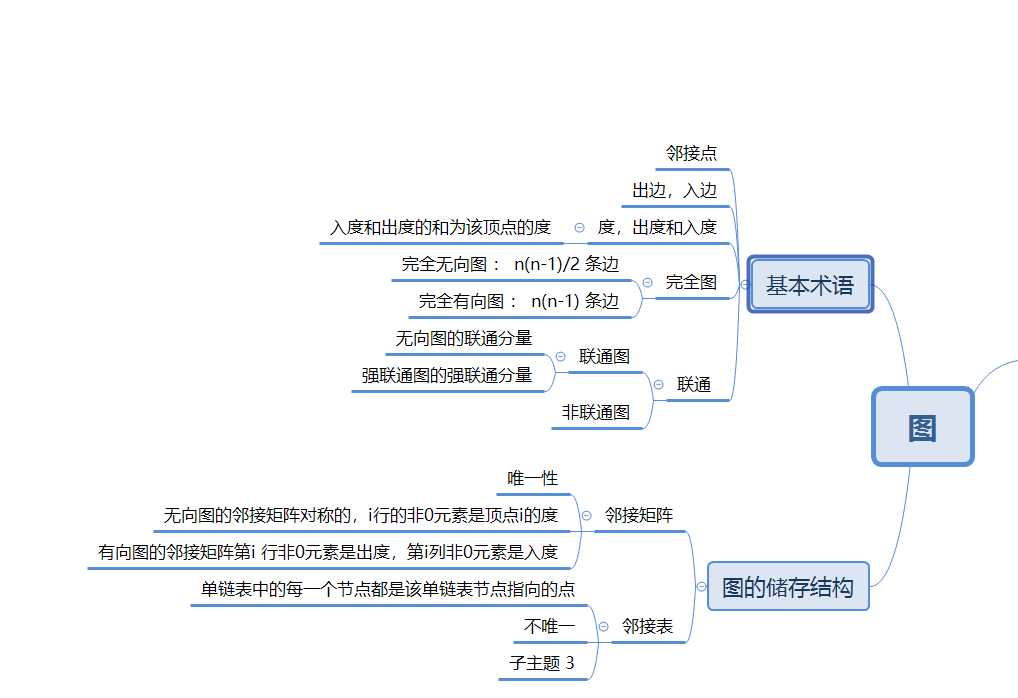
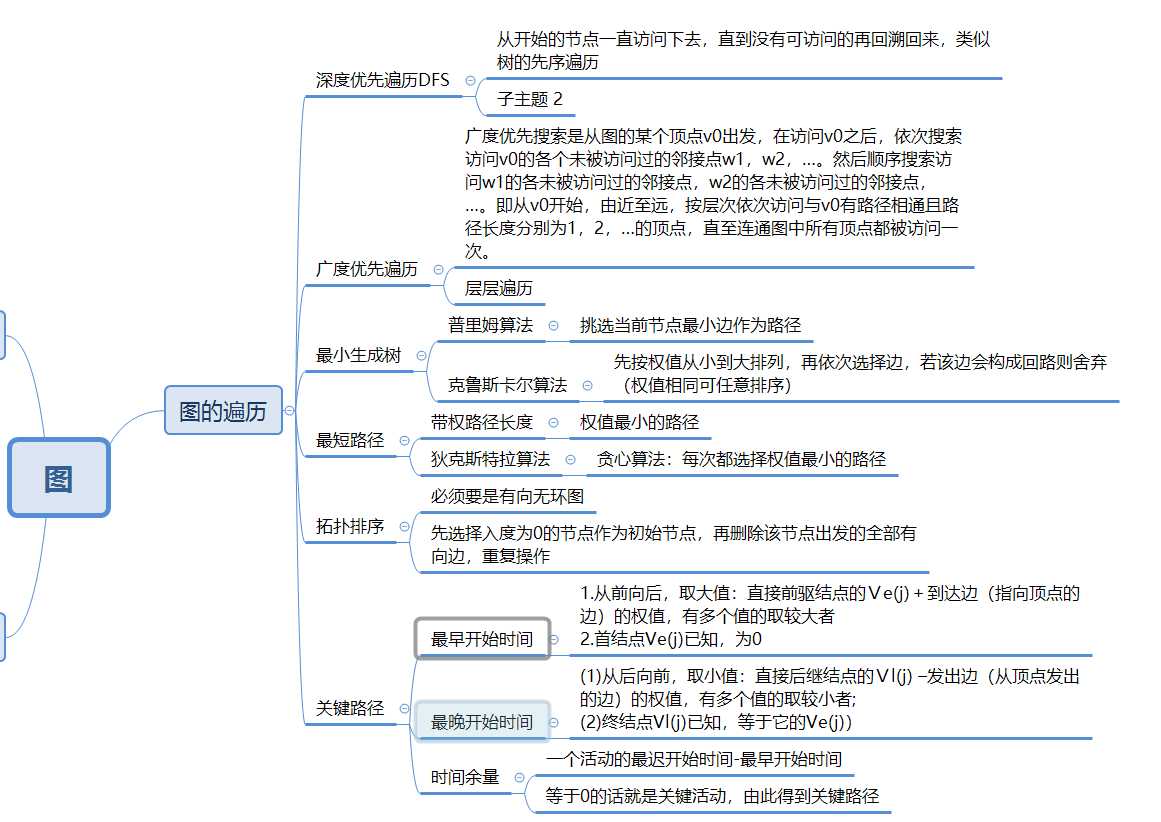
深度遍历算法 ： 沿着某一节点一直遍历下去直到没有后继节点，然后回溯，看是否还有节点没有遍历到，重复上述步骤，直到所有节点都被访问过了。如果图不联通，已经访问的节点都回溯完了，仍未找到为访问节点可以用visited[i] 数组查找 。
广度遍历算法 ： 如同树的层次遍历，一层一层访问节点 ，需要用到队列来储存每层的节点 ，先入队的先对他进行遍历 。
Prim和Kruscal算法 ：最小生成树算法 ： Prim算法从任意一个给定的节点开始，每次选择与当前节点集合中权重最小的节点，并将两节点之间的边加入到树中，应用贪心算法 。Kruscal算法 ：将每条边的权重按从小到大排列，按照权值的升序来选择边，选择边的同时要注意如果加入该边后形成了回路，就要把这条边删去，选择下一条。
Dijkstra算法 ：最短路径问题 ：初始时：先将初始节点与能到的节点之间边的权重记录在dis[]数组内，到不了的记为无穷大 。并用path[]数组记录下一条边的前驱节点作为路径,没有路径记为-1，然后在dis[]数组内选择最小值，则该值就是源点到达该值对应的顶点的最短路径，并把该节点记录到数组T中，在T新加入的节点寻找是否还有更小的边，有则修改dis数组中对应的值，以及path数组的路径 。
拓扑排序算法 ：在有向图中选一个没有前驱的顶点并且输出，同时将与节点有关的边标记删除。重复操作，若输出的节点数小于原有元素个数，则判定图有环 。

2.PTA实验作业（4分）

2.1 题目1：题目名称

4. 阅读代码（必做，1分）

迷宫问题(BFS:迷宫最短路径且输出路径)

#include<cstdio>  
#include<cstring>  
#include<algorithm>  
#include<queue>  
#include<stack>  
using namespace std;  
int maze[10][10];  
int vis[10][10],dist[10][10];  
int dr[]={-1,1,0,0};//上,下,左,右  
int dc[]={0,0,-1,1};  
struct Node  
{  
    int r,c;//也可以在Node中加一个int pre属性,然后做一个全局的nodes,就不用pre[][]数组了.  
    Node(int r,int c):r(r),c(c){}  
    Node(){}  
}pre[10][10];  
queue<Node> Q;  
void BFS()  
{  
    while(!Q.empty()) Q.pop();  
    memset(vis,0,sizeof(vis));  
    dist[0][0]=0;  
    vis[0][0]=1;  
    Q.push(Node(0,0));  
    while(!Q.empty())  
    {  
        Node node=Q.front();Q.pop();  
        int r=node.r,c=node.c;  
        for(int d=0;d<4;d++)  
        {  
            int nr=r+dr[d];  
            int nc=c+dc[d];  
            if(nr>=0&&nr<5&&nc>=0&&nc<5&&vis[nr][nc]==0&&maze[nr][nc]==0)  
            {  
                vis[nr][nc]=1;  
                Q.push(Node(nr,nc));  
                dist[nr][nc]=1+dist[r][c];  
                pre[nr][nc]=Node(r,c);  
                if(nr==4&&nc==4) return ;  
            }  
        }  
    }  
}  
int main()  
{  
    for(int i=0;i<5;i++)  
        for(int j=0;j<5;j++)  
            scanf("%d",&maze[i][j]);  
    BFS();  
    stack<Node> S;  
    int cur_r=4,cur_c=4;  
    while(true)  
    {  
        S.push(Node(cur_r,cur_c));  
        if(cur_r==0&&cur_c==0) break;  
        int r=cur_r,c=cur_c;  
        cur_r=pre[r][c].r;  
        cur_c=pre[r][c].c;  
    }  
    while(!S.empty())  
    {  
        Node node=S.top(); S.pop();  
        printf("(%d, %d)\n",node.r,node.c);  
    }  
    return 0;  
}  

直接BFS求解即可,需要用到vis数组和dist数组,用pre数组来保存当前节点的最短路径上的前一个点 .

博客作业06--图

原文：https://www.cnblogs.com/FOXES/p/9192129.html