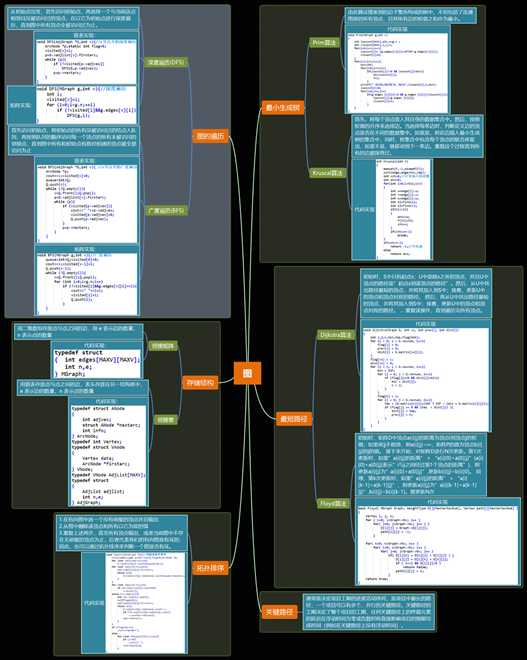
用二维数组 es[e][2] 存放输入的边集// e 是输入的行数
while (颜色分配方案 m-- 不为0)
color 数组存放每个结点对应的颜色,flag 等于 1 作为标志
用 map<int,int> col 统计输入颜色的个数
输入 color 数组的内容,并把对应的 col 内容置为1
if ( col 的元素个数不等于 k ) 输出 “No” ;
else
for(遍历边集 es )
if ( es 的同一行的两个元素对应的颜色相同 )
输出 “No”,flag 等于 0
if ( flag 为真 )
输出 “Yes”
end for
end while

MAX 定义为 1050
邻接矩阵 edge [MAX][MAX] ,Vnum 统计遍历过的结点数,sum 存放路径和
将 low 数组初始化为邻接矩阵中起始点的那一行
for i = 0 to n-1
min = MAX,k;
遍历 low 数组,找到数组中最小且不为 0 的边,将 min 定位到这个边的权重,k 定位到这个边在数组中的位置
if( min == MAX ) 说明没有边,结束循环
sum 加上最小边,low 数组中 k 位置设为 0 ,Vnum 记录遍历的结点数
for j = 1 to n
if( low[j] 存在且 edge[k][j] 小于 low[j] )把 low[j] 的值更新为 edge[k][j] 的值
end for j
end for i
if ( Vnum 不等于 n )输出 -1
else 输出 sum 的值

if (min==MAX)一句,然后就错了。 MAX 取值为 550
邻接矩阵 edge[MAX][MAX] 存放 距离 权重;邻接矩阵 costs[MAX][MAX] 存放 路费 权重,最短路径数组 dist[MAX],最小花费数组 cost[MAX],记录遍历结点的数组 visited[MAX] = { 0 }
将 dist 数组初始化为初始点的 edge 的那一行,cost 数组初始化为初始点的 costs 的那一行
将初始点的 dist 归零,对应的 visited 数组位置置为 1
for i = 0 to n-2
min = MAX,k;
遍历 dist 数组,找到数组中最小且对应结点未被遍历的边,将 min 定位到这个边的权重,k 定位到这个边在数组中的位置
将 k 结点的 visited 置为 1
for j = 0 to n-1
if( j 结点未被遍历且初始点到 k 结点的距离加上 k 结点到 j 结点的距离比初始点到 j 结点的距离小) 更新 dist[j] 为 dist[k]+edge[k][j]
else if( j 结点未被遍历且 dist[j] == dist[k]+edge[k][j] 且 costs[k][j]+cost[k] 小于 cost[j] ) 更新 cost[j] 为 costs[k][j]+cost[k]
end for j
end for i


原文:https://www.cnblogs.com/linyue711/p/9178283.html