Rorigin?Ro?[Xo Yo Zo]
Rdirection?Rd?[Xd Yd Zd]
当xd2+yd2+zd2=1 (i.e normalized)
他定义了一个光线:
即一个线上的点集 R(t)=Ro+Rd*t where t>0 (A1)
t<0的点全在光线源点后。至于t=0为什么不被当做光线上的点,这个问题将会放到‘精度问题‘的章节来解释。注意,虽然光线方向不需要进行标准化,但是还是建议使用标准化,否通,t将用方向向量的长度来表示距离。在相交测试前,对光线方向向量进行一次标准化。,以确保t将等于从光线原点到世界坐标系的距离。
A1是光线方程的参数或者说是显式形式。这意味着光线上所有的点都可以通过改变t的值直接生成。
球体定义:
球心?Sc?[Xc Yc Zc]
半径?Sr
表面集合?[Xs Ys Zs] where (Xs-Xc)2+(Ys-Yc)2+(Zs-Zc)2=Sr2 (A2)
曲面上的点不能直接生成,每个点都应该用隐式方程进行检测,如果满足条件,才是在曲面上的点。
A1表示为方程组:
X=Xo+Xd*t
Y=Yo+Yd*t
Z=Zo+Zd*t
将球面[Xs Ys Zs]带入A1方程组:
(Xo+Xd*t-Xc)2+(Yo+Yd*t-Yc)2+(Zo+Zd*t-Zc)2=Sr2
简化为:
A*t2+B*t+C=0 (A5)
A=Xd2+Yd2+Zd2=1
B=2*(Xd*(Xo-Xc)+Yd*(Yo-Yc)+Zd*(Zo-Zc))
C=(Xs-Xc)2+(Ys-Yc)2+(Zs-Zc)2-Sr2
注意A的系数(coefficient)一直为1,因为光线方向是标准化方向。
解A5方程:
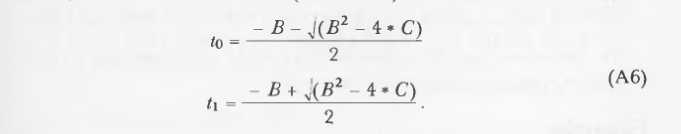
b2-4ac<0,无交点。 【在[11]的5.5节有t0,t1更准确的提纯方式】
t中更小的正实根时光线上最近的交点距离,即t*B最短。
一旦t求出,则可推导实际的交点:
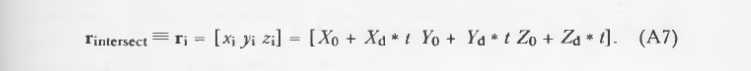
=》曲面上的单位法向量可以很简单得出:
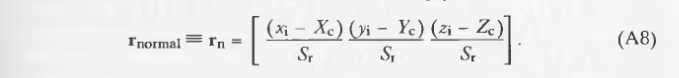
如果光源在球内,那么rn应该取反,以便它指向光线。
总结起来,代数解法步骤为:
1,计算方程的A,B,C
2,计算判别式(△)
3,t0的计算和比较
4,也许还有t1的ca,co
5,计算交点
6,计算法线
原文:https://www.cnblogs.com/TooYoungTsukasa/p/9206722.html