[TOC]
此篇博客大部分内容来自于 hihoCoder , 借此学习 !! (侵删)
以后博客的 markdown 风格会进行改变qwq 主要是找到了新的 typora 用法 2333
对于一个字符串 \(S\) ,它对应的后缀自动机是一个最小的确定有限状态自动机(DFA),接受且只接受 \(S\) 的后缀。
比如对于字符串 \(S=\underline{aabbabd}\),它的后缀自动机是
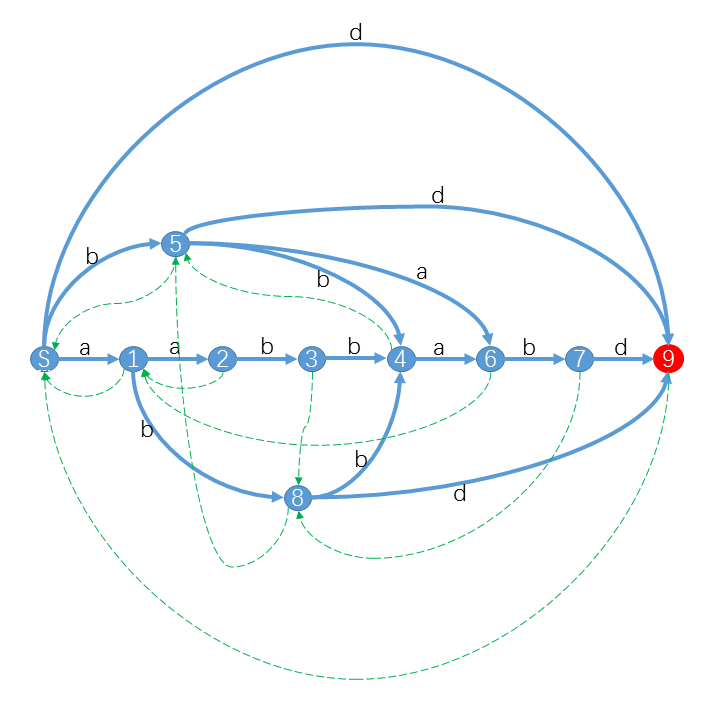
其中 红色状态 是终结状态。你可以发现对于S的后缀,我们都可以从S出发沿着字符标示的路径( 蓝色实线 )转移,最终到达终结状态。
特别的,对于S的子串,最终会到达一个合法状态。而对于其他不是S子串的字符串,最终会“无路可走”。
我们知道 \(SAM\) 本质上是一个 \(DFA\) ,\(DFA\) 可以用一个五元组 <字符集、状态集、转移函数、起始状态、终结状态集> 来表示。至于那些 绿色虚线 虽然不是DFA的一部分,却是SAM的重要部分,有了这些链接 \(SAM\) 是如虎添翼,我们后面再细讲。
其中比较重要的是 状态集 和 转移函数 .
首先我们先介绍一个概念 子串的结束位置 集合 \(endpos\) 。
对于 \(S\) 的一个子串 \(s\) ,\(endpos(s) = s\) 在 \(S\) 中所有出现的结束位置集合。
还是以 \(S=\underline{aabbabd}\) 为例,\(endpos(\underline{ab}) = \{3, 6\}\) ,因为 \(\underline{ab}\) 一共出现了 \(2\) 次,结束位置分别是 \(3\) 和 \(6\) 。同理 \(endpos(\underline{a}) = \{1, 2, 5\}\) , \(endpos(\underline{abba}) = \{5\}\) 。
我们把 \(S\) 的所有子串的 \(endpos\) 都求出来。如果两个子串的 \(endpos\) 相等,就把这两个子串归为一类。最终这些 \(endpos\) 的等价类就构成的 \(SAM\) 的状态集合。
1.令 \(s_1,s_2\) 为 \(S\) 的两个子串 ,不妨设 \(|s_1|\le|s_2|\) (我们用 \(|s|\) 表示 \(s\) 的长度 ,此处等价于 \(s_1\) 不长于 \(s_2\) )。则 \(s_1\) 是 \(s_2\) 的后缀当且仅当 \(endpos(s_1) \supseteq endpos(s_2)\) ,\(s_1\) 不是 \(s_2\) 的后缀当且仅当 \(endpos(s_1) \cap endpos(s_2) = \emptyset\) 。
这个证明是很显然的 :
首先证明 \(s_1\) 是 \(s_2\) 的后缀 \(\Rightarrow\) \(endpos(s_1) \supseteq endpos(s_2)\) 。
因为每次出现 \(s_2\) 时候,\(s_1\) 一定会伴随出现。然后证明 \(endpos(s_1) \supseteq endpos(s_2)\) \(\Rightarrow\) \(s_1\) 是 \(s_2\) 的后缀 。显然 \(endpos(s_2) \not = \emptyset\) ,那么意味着每次 \(s_2\) 结束的时候 \(s_1\) 也会结束,且 \(|s_1| \le |s_2|\) ,那么显然成立。
所以这两个互为充要条件。那么 \(s_1\) 不是 \(s_2\) 的后缀当且仅当 \(endpos(s_1) \cap endpos(s_2) = \emptyset\) 就是其中的推论了,后者是前者的必要条件。
2.\(SAM\) 中的一个状态包含的子串都具有相同的 \(endpos\),它们都互为后缀。
其中一个状态指的是从起点开始到这个点的所有路径组成的子串的集合。
例如上图中状态 \(4\) 为 \(\{\underline{bb},\underline{abb},\underline{aabb}\}\) 。
3.我们用 \(substrings(st)\) 表示状态 \(st\) 中包含的所有子串的集合,\(longest(st)\) 表示 \(st\) 包含的最长的子串,\(shortest(st)\)表示\(st\)包含的最短的子串。
例如对于状态 \(7\) ,\(substring(7)=\{\underline{aabbab},\underline{abbab},\underline{bbab},\underline{bab}\}\),\(longest(7)=\underline{aabbab}\),\(shortest(7)=\underline{bab}\) 。
那么有 对于一个状态 \(st\) ,以及任意 \(s\in substrings(st)\) ,都有 \(s\) 是 \(longest(st)\) 的后缀。
证明比较容易,因为 \(endpos(s)=endpos(longest(st)) ~|s| \le |st|\) ,所以 \(endpos(s) ? endpos(longest(st))\) ,根据我们刚才证明的结论有 \(s\) 是 \(longest(st)\) 的后缀。
4.对于一个状态 \(st\) ,以及任意的 \(longest(st)\) 的后缀 \(s\) ,如果 \(s\) 的长度满足:\(|shortest(st)| \le |s| \le |longsest(st)|\) ,那么 \(s \in substrings(st)\) 。
其实是定义然后很显然?证明有:\(|shortest(st)| \le|s|\le|longsest(st)|\)> ,所以\(endpos(shortest(st)) \supseteq endpos(s) \supseteq endpos(longest(st))\) ,又 \(endpos(shortest(st))=endpos(longest(st))\) 所以 \(endpos(shortest(st)) = endpos(s) = endpos(longest(st))\) ,所以 \(s\in substrings(st)\) 。
也就是说 \(substrings(st)\) 包含的是 \(longest(st)\) 的一系列连续后缀。
例如 状态 \(7\) 中包含的就是 \(\underline{aabbab}\) 的长度分别是 \(6,5,4,3\) 的后缀;状态 \(6\) 包含的是 \(\underline{aabba}\) 的长度分别是 \(5,4,3,2\) 的后缀。
前面我们讲到 \(substrings(st)\) 包含的是 \(longest(st)\) 的一系列连续后缀。这连续的后缀在某个地方会“断掉”。
比如状态 \(7\) ,包含的子串依次是 \(\underline{aabbab},\underline{abbab},\underline{bbab},\underline{bab}\) 。按照连续的规律下一个子串应该是 \(\underline{ab}\) ,但是 \(\underline{ab}\) 没在状态 \(7\) 里。
这是为什么呢?
\(\underline{aabbab},\underline{abbab},\underline{bbab},\underline{bab}\) 的 \(endpos\) 都是 \(\{6\}\) ,下一个 \(\underline{ab}\) 当然也在结束位置 \(6\) 出现过,但是 \(\underline{ab}\) 还在结束位置 \(3\) 出现过,所以 \(\underline{ab}\) 比 \(\underline{aabbab},\underline{abbab},\underline{bbab},\underline{bab}\) 出现次数更多,于是就被分配到一个新的状态中了。
当 \(longest(st)\) 的某个后缀 \(s\) 在新的位置出现时,就会“断掉”,\(s\) 会属于新的状态。
比如上例中 \(\underline{ab}\) 就属于状态 \(8\) ,\(endpos(\underline{ab})=\{3,6\}\) 。当我们进一步考虑 \(\underline{ab}\) 的下一个后缀 \(\underline{b}\) 时,也会遇到相同的情况:\(\underline{b}\) 还在新的位置 \(4\) 出现过,所以 \(endpos(\underline{b})=\{3,4,6\}\) ,\(\underline{b}\) 属于状态 \(5\) 。在接下去处理 \(\underline{b}\) 的后缀我们会遇到空串, \(endpos(\underline{})= \{0,1,2,3,4,5,6\}\) ,状态是起始状态 \(S\) 。
于是我们可以发现一条状态序列: \(7 \to 8 \to 5 \to S\) 。这个序列的意义是 \(longest(7)\) 即 \(\underline{aabbab}\) 的后缀依次在状态 \(7,8,5,S\) 中。我们用后缀链接 \(Suffix Link\) 这一串状态链接起来,这条 \(link\) 就是上图中的绿色虚线。
后面这个会有妙用qwq
最后我们来介绍 \(SAM\) 的转移函数。对于一个状态 \(st\) ,我们首先找到从它开始下一个遇到的字符可能是哪些。我们将 \(st\) 遇到的下一个字符集合记作 \(next(st)\) ,有 \(next(st) = \{S[i+1] | i \in endpos(st)\}\) 。例如 \(next(S)=\{S[1], S[2], S[3], S[4], S[5], S[6], S[7]\}=\{a, b, d\}\) ,\(next(8)=\{S[4], S[7]\}=\{b, d\}\) 。
比如对于状态 \(4\) ,\(next(4)=\{a\}\) ,\(\underline{aabb},\underline{abb},\underline{bb}\) 后面接上字符 \(\underline{a}\) 得到 \(\underline{aabba},\underline{abba},\underline{bba}\) ,这些子串都属于状态 \(6\) 。
所以我们对于一个状态 \(st\) 和一个字符 \(c\in next(st)\) ,可以定义转移函数 \(trans(st, c) = \{x | longest(st) + c \in substrings(x) \}\) 。换句话说,我们在 \(longest(st)\)(随便哪个子串都会得到相同的结果)后面接上一个字符 \(c\) 得到一个新的子串 \(s\) ,找到包含 \(s\) 的状态 \(x\) ,那么 \(trans(st, c)\) 就等于\(x\) 。
\(SAM\) 有 \(O(|S|)\) 的构造方法,接下来我们讲讲如何构造。
首先为了实现 \(O(|S|)\) 的构造,对于每个状态肯定不能保存太多数据。例如 \(substrings(st)\) 肯定无法保存下来了。
对于状态 \(st\) 我们只保存如下数据:
| 数据 | 含义 |
|---|---|
| \(maxlen[st]\) | \(st\) 包含的最长子串的长度 |
| \(minlen[st]\) | \(st\) 包含的最短子串的长度 |
| \(trans[st][]\) | \(st\) 的转移函数 |
| \(link[st]\) | \(st\) 的后缀链接 |
其次,我们使用增量法构造 \(SAM\) 。我们从初始状态开始,每次考虑添加一个字符 \(S[1],S[2],...,S[N]\) ,依次构造可以识别 \(S[1], S[1..2], S[1..3], \cdots ,S[1..N]=S\) 的 \(SAM\) 。
假设我们已经构造好了 \(S[1..i]\) 的 \(SAM\) 。这时我们要添加字符 \(S[i+1]\) ,于是我们新增了 \(i+1\) 个 \(S[i+1]\) 的后缀要识别:\(S[1..i+1], S[2..i+1], ... S[i..i+1], S[i+1]\) 。 考虑到这些新增状态分别是从 \(S[1..i], S[2..i], S[3..i], \cdots , S[i], \underline{}\) (空串)通过字符 \(S[i+1]\) 转移过来的,所以我们还要对 \(S[1..i], S[2..i], S[3..i], \cdots , S[i], \underline{}\) (空串) 对应的状态们增加相应的转移。
我们假设 \(S[1..i]?\) 对应的状态是 \(u?\) ,等价于 \(S[1..i]\in substrings(u)?\) 。根据上面的讨论我们知道 \(S[1..i], S[2..i], S[3..i], ... , S[i], \underline{}?\) (空串)对应的状态们恰好就是从 \(u?\) 到初始状态 \(S?\) 的由 \(Suffix Link?\) 连接起来路径上的所有状态,不妨称这条路径(上所有状态集合)是 \(suffix-path(u\to S)?\) 。
原文:https://www.cnblogs.com/zjp-shadow/p/9218214.html