#include <iostream>
using namespace std;
int part(int a[], int i, int j)
{
int tmp = a[i];
if(i < j)
{
while(i < j)
{
while(i<j && a[j]>=tmp)
j--;
if(i < j)
a[i] = a[j];
while(i<j && a[i]<tmp)
i++;
if(i < j)
a[j] = a[i];
}
a[i] = tmp;
return i;
}
}
int check(int a[], int i, int j, int k)
{
int m = part(a, i, j);
if(k == m-i+1)
return a[m];
else if(k < m-i+1)
return check(a, i, m-1, k);
else
return check(a, m+1, j, k-(m-i+1));
}
int main()
{
int a[9] = {3,2,6,5,7,8,9,1,0};
int k = 0;
cout << check(a, 0, 8, 9-k)<< endl;
return 0;
}
.只需找到第k大的数,不必把所有的数排好序。我们借助快排中partition过程,一般情况下,在把所有数都排好序前,就可以找到第k大的数。我们依据的逻辑是,经过一次partition后,数组被pivot分成左右两部分:S左、S右。当S左的元素个数|S左|等于k-1时,pivot即是所找的数;当|S左|小于k-1,所找的数位于S右中;当|S左|>k-1,所找的数位于S左中。显然,后两种情况都会使搜索空间缩小。
算法的时间复杂度为:O(N),计算公式,假设我们的数据足够的随机,每次划分都在数据序列的中间位置,根据条件1,那么第一次划分我们需要遍历约n个数,第二次需要遍历约n/2个数,...,这样递归下去,最后:
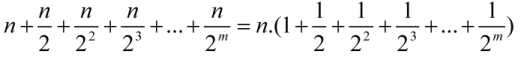
原文:https://www.cnblogs.com/ya-cpp/p/9245065.html