一 题意描述:
给定由n个要相乘的矩阵构成的序列(链)<A1,A2,A3,····An>。由于矩阵满足结合律(加括号方式表示结合方式),不同的计算方式导致的求出最终计算结果的代价相异,有的花的时间很少,有的方式所花时间很多,那么下面的任务就是求出算出结果所需要的最少时间及一个最优解。
二 思路分析:
设p(n)表示一串n个矩阵可能的加全部括号方案数。当n=1时,只有一个矩阵,此时p(1)=1。当n>=2时,一个加全部括号的矩阵乘积等于两个加全部括号的子矩阵乘积的乘积,而且这两个子乘积之间的分裂可能发生在第k个和第k+1个矩阵之间,其中k=1,2,····,n-1;因此可以求得递归式:
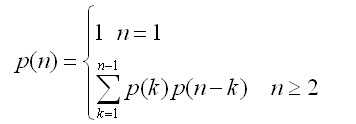
1.找局部最优解:把问题: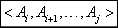 转化成两个最优子问题:
转化成两个最优子问题: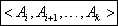 及
及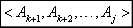
2.构造递归解:
首先定义m[i,j]为解决子问题A[i....j]的最小计算次数,那么解决整个问题A[1,n]所花的最小时间为m[1,n]。
那么递归方程可以写成如下形式:
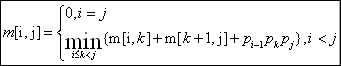
为了跟踪如何构造一个最优解我们可以定义s[i,j]为这样的一个k值,在该处分裂乘积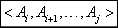 后可得一个最优解。
后可得一个最优解。
3.构造函数进行求解

输出最优路径的函数自己编写,经过调用数组s[i][j]即可。
原文:http://www.cnblogs.com/khbcsu/p/3857028.html