一、决策树
决策树是什么?决策树(decision tree)是一种基本的分类与回归方法。举个通俗易懂的例子,如下图所示的流程图就是一个决策树,长方形代表判断模块(decision block),椭圆形成代表终止模块(terminating block),表示已经得出结论,可以终止运行。从判断模块引出的左右箭头称作为分支(branch),它可以达到另一个判断模块或者终止模块。我们还可以这样理解,分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类。蒙圈没??如下图所示的决策树,长方形和椭圆形都是结点。长方形的结点属于内部结点,椭圆形的结点属于叶结点,从结点引出的左右箭头就是有向边。而最上面的结点就是决策树的根结点(root node)。这样,结点说法就与模块说法对应上了,理解就好。
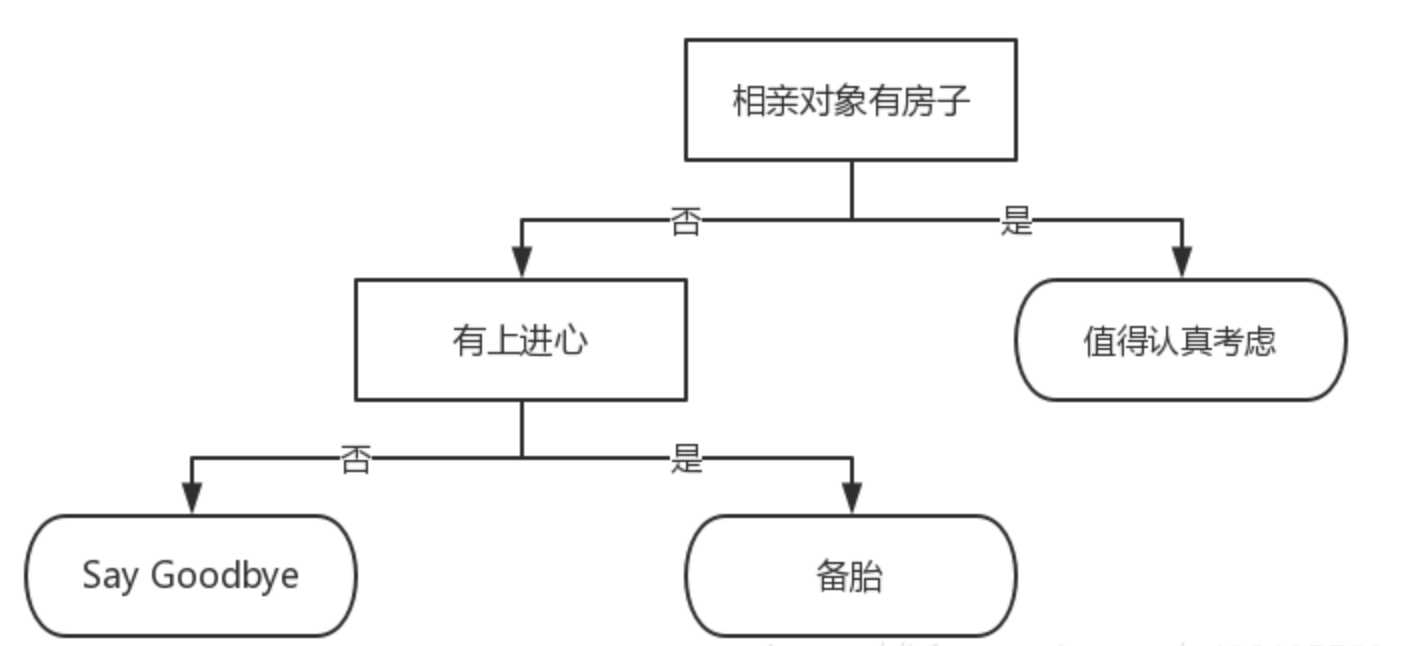
我们回到这个流程图,对,你没看错,这就是一个假想的相亲对象分类系统。它首先检测相亲对方是否有房。如果有房,则对于这个相亲对象可以考虑进一步接触。如果没有房,则观察相亲对象是否有上进心,如果没有,直接Say Goodbye,此时可以说:”你人很好,但是我们不合适。”如果有,则可以把这个相亲对象列入候选名单,好听点叫候选名单,有点瑕疵地讲,那就是备胎。
不过这只是个简单的相亲对象分类系统,只是做了简单的分类。真实情况可能要复杂得多,考虑因素也可以是五花八门。脾气好吗?会做饭吗?愿意做家务吗?家里几个孩子?父母是干什么的?
我们可以把决策树看成一个if-then规则的集合,将决策树转换成if-then规则的过程是这样的:由决策树的根结点(root node)到叶结点(leaf node)的每一条路径构建一条规则;路径上内部结点的特征对应着规则的条件,而叶结点的类对应着规则的结论。决策树的路径或其对应的if-then规则集合具有一个重要的性质:互斥并且完备。这就是说,每一个实例都被一条路径或一条规则所覆盖,而且只被一条路径或一条规则所覆盖。这里所覆盖是指实例的特征与路径上的特征一致或实例满足规则的条件。
二、决策树构建的准备工作
决策树要如何构建呢?通常,这一过程可以概括为3个步骤:特征选择、决策树的生成和决策树的修剪。
2.1 特征选择
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率,如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则称这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的标准是信息增益(information gain)或信息增益比
2.1.1 香农熵
集合信息的度量方式成为香农熵或者简称为熵(entropy),这个名字来源于信息论之父克劳德·香农。
熵定义为信息的期望值。在信息论与概率统计中,熵是表示随机变量不确定性的度量。如果待分类的事务可能划分在多个分类之中,则符号xi的信息定义为
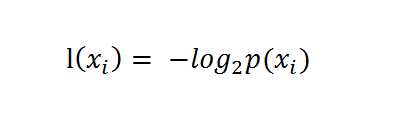
其中p(xi)是选择该分类的概率。
通过上式,我们可以得到所有类别的信息。为了计算熵,我们需要计算所有类别所有可能值包含的信息期望值(数学期望),通过下面的公式得到:
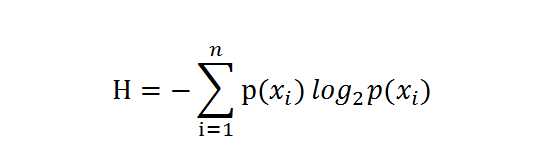
期中n是分类的数目。熵越大,随机变量的不确定性就越大。
2.1.2 编写代码计算熵
我们已经学会了通过公式计算熵,接下来编写代码,计算熵
1 # coding=utf-8 2 from math import log 3 4 5 # 数据集创建 6 def createDataSet(): 7 dataSet = [ 8 [1, 1, ‘yes‘], [1, 1, ‘yes‘], [1, 0, ‘no‘], [0, 1, ‘no‘], [0, 1, ‘no‘] 9 ] 10 labels = [‘no surfacing‘, ‘flippers‘] 11 return dataSet, labels 12 13 14 # 计算给定数集的香农熵 15 def calcShannonEnt(data_set): 16 numEntries = len(data_set) 17 labelCounts = {} 18 for featVec in data_set: 19 currentLabel = featVec[-1] 20 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 21 labelCounts[currentLabel] += 1 22 shannonEnt = 0.0 23 for key in labelCounts: 24 prob = float(labelCounts[key]) / numEntries 25 shannonEnt -= prob * log(prob, 2) 26 return shannonEnt 27 28 29 myData, labels = createDataSet() 30 print(myData) 31 print(calcShannonEnt(myData)) 32 33 myData[0][-1] = ‘maybe‘ 34 print(myData) 35 print(calcShannonEnt(myData))
原文:https://www.cnblogs.com/zcjcsl/p/9206811.html