朋友面试遇到一道笔试题:写出递归遍历二叉树的代码(先序、中序、后序遍历都可以)?
首先要知道二叉树是什么,它的数据结构是怎样的?
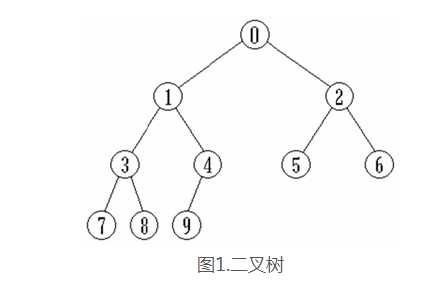
如何实现这种二叉树?采用匿名内部类的形式实现
class Node{
//节点数据
private T data; //可比较的泛型
//左子树
private Node leftChildTree;
//右子树
private Node rightChildTree;
public Node(T data){
this.data = data;
}
}
知道它的数据类型就容易对其进行遍历
//前序遍历 public void preorderTraversal(Node root){ if (root == null){ return; } System.out.println("node = [" + root.data + "]"); preorderTraversal(root.leftChildTree); preorderTraversal(root.rightChildTree); } //中序遍历 public void inorderTraversal(Node root){ if (root == null){ return; } inorderTraversal(root.leftChildTree); System.out.println("node = [" + root.data + "]"); inorderTraversal(root.rightChildTree); } //后续遍历 public void postorderTraversal(Node root){ if (root == null){ return; } postorderTraversal(root.leftChildTree); postorderTraversal(root.rightChildTree); System.out.println("node = [" + root.data + "]"); }
但真的这么简单么?
数据结构和算法问题,解决问题只是看储备知识的广度,优化问题才是看能力素质的高度
栈模拟递归的非递归算法:这样算法空间复杂度为O(h),h为二叉树的高度

//前序遍历 public void preorderTraversal(Node root){ if (root == null){ return; } Stack<Node> stack = new Stack<Node>(); stack.push(root); while (!stack.empty()){ Node node = stack.pop(); System.out.println("node = [" + node.data + "]"); if (root.rightChildTree != null) stack.push(root.rightChildTree); if (root.leftChildTree != null) stack.push(root.leftChildTree); } } //中序遍历 public void inorderTraversal(Node root){ if (root == null){ return; } Stack<Node> stack = new Stack<Node>(); Stack<Node> stack2 = new Stack<Node>(); stack.push(root); while (!stack.empty()){ if (root.rightChildTree != null) stack.push(root.rightChildTree); Node node = stack.pop(); stack2.push(node); if (root.leftChildTree != null) stack.push(root.leftChildTree); } while(!stack2.empty()) { Node node2 = stack2.pop(); System.out.println("node = [" + node2.data + "]"); } } //后续遍历 public void postorderTraversal(Node root){ if (root == null) return; Stack<Node> stack = new Stack<Node>(); Stack<Node> stack2 = new Stack<Node>(); stack.push(root); while (!stack.empty()) { Node node = stack.pop(); stack2.push(node); if (root.rightChildTree != null) stack.push(root.rightChildTree); if (root.leftChildTree != null) stack.push(root.leftChildTree); } while(!stack2.empty()) { Node node2 = stack2.pop(); System.out.println("node = [" + node2.data + "]"); } }
Morris遍历的神奇之处在于它是非递归的算法,但并不需要额外的O(h)的空间,而且复杂度仍然是线性的。
Morrs遍历优势:O(1)空间复杂度;二叉树的形状不被破坏
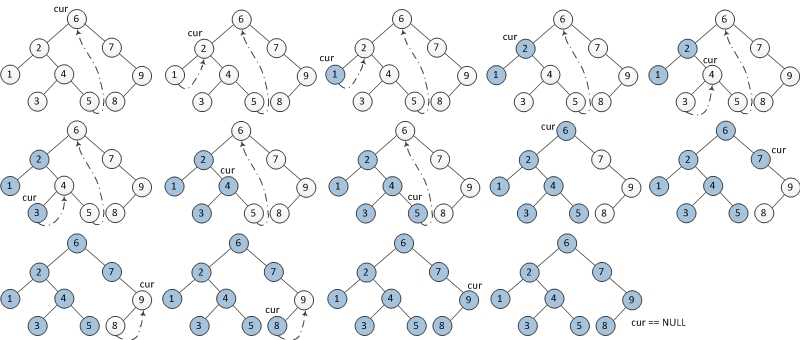
1、先找到根节点的左子树的最右节点,让最右节点的右子树指向根节点。(本来最右节点的右子树是null,将根节点复制给它)
4、以左子树的根节点的为根节点,继续1步骤。
3、然后中序遍历:当左子树为空时,打印输出,
当节点指向的右子树等于根节点时,说明此节点为根节点左子树的最右节点,打印根节点,遍历右子树。

//中序遍历 public void inorderTraversal(Node root){ if (root == null){ return; } Node node = root; while (node != null){ if (node.leftChildTree == null){ System.out.println("node = [" + node.data + "]"); node = node.rightChildTree; }else { Node temp = node.leftChildTree; while (temp.rightChildTree != null && temp.rightChildTree != temp){ temp = temp.rightChildTree; } if (temp.rightChildTree == null){ temp.rightChildTree = node; node = node.leftChildTree; }else{ temp.rightChildTree = null; System.out.println("node = [" + node.data + "]"); node = node.rightChildTree; } } } }
解决了这道题,我们再扩展一下,看一下一个二叉树结构都应该有哪些功能呢?
基本操作:树的主要操作有
(1)创建树IntTree(&T)
(2)销毁树DestroyTree(&T)
(3)构造树CreatTree(&T,deinition)
(4)置空树ClearTree(&T)
(5)判空树TreeEmpty(T)
(6)求树的深度TreeDepth(T)
(7)获得树根Root(T)
(8)获取结点Value(T,cur_e,&e),将树中结点cur_e存入e单元中。
(9)数据赋值Assign(T,cur_e,value),将结点value,赋值于树T的结点cur_e中。
(10)获得双亲Parent(T,cur_e),返回树T中结点cur_e的双亲结点。
(11)获得最左孩子LeftChild(T,cur_e),返回树T中结点cur_e的最左孩子。
(12)获得右兄弟RightSibling(T,cur_e),返回树T中结点cur_e的右兄弟。
(13)插入子树InsertChild(&T,&p,i,c),将树c插入到树T中p指向结点的第i个子树之前。
(14)删除子树DeleteChild(&T,&p,i),删除树T中p指向结点的第i个子树。
(15)遍历树TraverseTree(T,visit())
原文:https://www.cnblogs.com/syd-fish-cat/p/9265521.html