2018-07-12 23:21:53
问题描述:
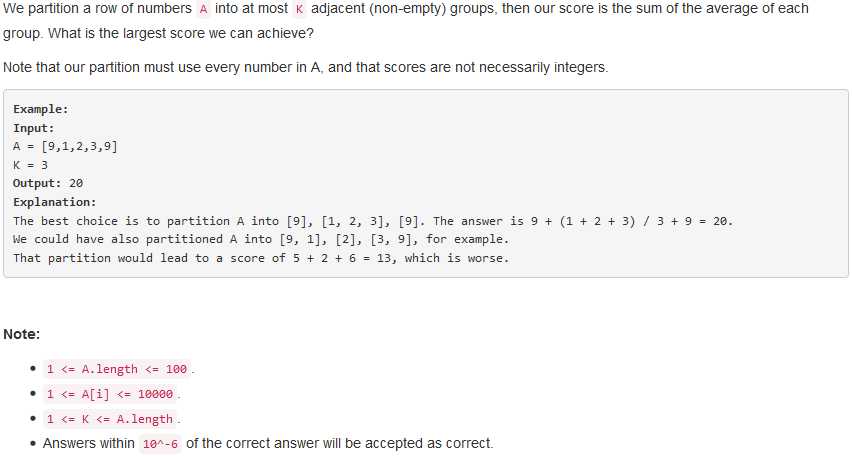
问题求解:
dp[i][j] : 以ai结尾的分j个部分得到的最大值
dp[i][j] = max{dp[k][j - 1] + (ak+1 + ... + ai) / (i - k)} k = [j - 2, i - 1]
public double largestSumOfAverages(int[] A, int K) {
double[][] dp = new double[A.length][K + 1];
int sum = 0;
for (int i = 0; i < A.length; i++) {
sum += A[i];
dp[i][1] = sum * 1.0 / (i + 1);
}
for (int j = 2; j < K + 1; j++) {
for (int i = j - 1; i < A.length; i++) {
for (int k = j - 2; k < i; k++) {
sum = 0;
int temp = k + 1;
while (temp <= i) sum += A[temp++];
double avg = sum * 1.0 / (i - k);
dp[i][j] = Math.max(dp[i][j], dp[k][j - 1] + avg);
}
}
}
return dp[A.length - 1][K];
}
原文:https://www.cnblogs.com/TIMHY/p/9302493.html