一、什么是正则化
正则化即为对学习算法的修改,旨在减少泛化误差而不是训练误差。正则化的策略包括:
(1)约束和惩罚被设计为编码特定类型的先验知识
(2)偏好简单模型
(3)其他形式的正则化,如:集成的方法,即结合多个假说解释训练数据
在实践中,过于复杂的模型不一定包含数据的真实的生成过程,甚至也不包括近似过程,这意味着控制模型的复杂程度不是一个很好的方法,或者说不能很好的找到合适的模型的方法。实践中发现的最好的拟合模型通常是一个适当正则化的大型模型。
二、参数范数模型
对于线性模型,譬如线性回归、逻辑回归,可以使用简单有效的参数范数模型进行正则化。许多正则化方法通过对目标函数J添加惩罚项,限制模型的学习能力:
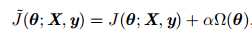
对于神经网络中,参数通常是包括权值w和偏置b,而我们通常对w做惩罚而不对偏置b做处理,这是因为不对b进行处理也不会有太大的影响。
2.1 L1正则和L2正则
L1正则项表示:
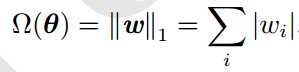
L2正则项表示:
![]()
2.2 为什么通过L1正则、L2正则能够防止过拟合
解释1:
过拟合产生的原因通常是因为参数比较大导致的,通过添加正则项,假设某个参数比较大,目标函数加上正则项后,也就会变大,因此该参数就不是最优解了。
问:为什么过拟合产生的原因是参数比较大导致的?
答:过拟合,就是拟合函数需要顾忌每一个点,当存在噪声的时候,原本平滑的拟合曲线会变得波动很大。在某些很小的区间里,函数值的变化很剧烈,这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大。
解释2:
对于L2正则,其目标函数为:
![]()
进一步做简化分析,令w*作为未正则化的目标函数取得最小值时的权重向量(当然这个值是有可能会过拟合的),在w*的邻域对目标函数做二次近似(泰勒展开,因为极值点的导数为0,因此一阶项为0),其中用H表示该函数的Hessian矩阵(关于w),其表达式为:
![]()
当它取得最小值时,其梯度为0,梯度表达式:
![]()
为了研究权重衰减带来的影响,添加权重衰减的梯度,使用![]() 表示此时的最优点:
表示此时的最优点:
![]()
![]()
可以看到,当α趋向于0时,正则化的解和未正则化的解相近;当α增加时,会怎样呢?因为H是实对称的,可以分解为一个对角矩阵Λ和一组特征向量的标注正交基Q。
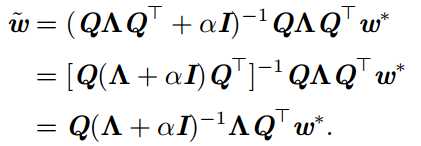
可以看到,权重衰减的效果是沿着由H的特征向量所定义的轴缩放w*。
原文:https://www.cnblogs.com/pinking/p/9310728.html