给定一正整数n,对n个点有标号的有向无环图(可以不连通)进行计数,输出答案mod 998244353的结果
考虑 \(O(n^2)\) DP
枚举出度为 \(0\) 的点,构成的新\(DAG\)方案数为
\(f[i]=f[i-1]*C_{n}^{1}*2^{n-1}\)
即从 \(n\) 个点中选出一个点,作为出度为 \(0\) 的点,然后剩下 \(n-1\) 个点向这个点任意连边
但是 \(f[i-1]\) 中也会有出度为 \(0\) 的点,那么就算重了,考虑容斥这个算重的东西
\(f[n]=\sum_{i=1}^{n}(-1)^{i+1}**f[i-j]*C_{i}^{j}*2^{j*(i-j)}\)
即至少有一个出度为 \(0\) 的点-至少有两个的+....
这个式子可以 分治+\(NTT\) 优化
只需要拆 \(2^{j*(i-j)}\) 这个东西就行了
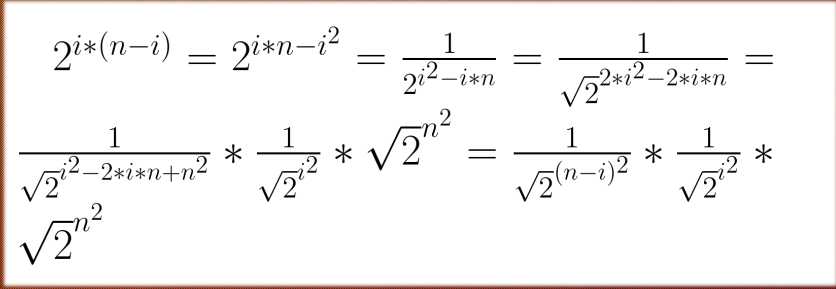
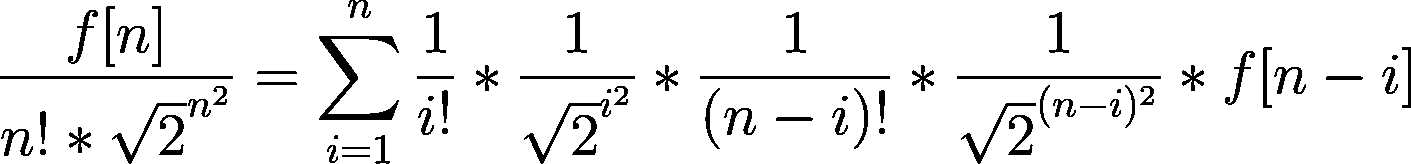
\(\sqrt(2)\) 的逆元可以枚举求出来
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4e5+10,G=116195171,mod=998244353;
inline int qm(int x,ll k){
int sum=1;
while(k){
if(k&1)sum=1ll*sum*x%mod;
x=1ll*x*x%mod;k>>=1;
}
return sum;
}
inline int inv(int x){return qm(x,mod-2);}
int n,m,R[N];
inline void NTT(int *A){
for(int i=0;i<n;i++)if(i<R[i])swap(A[i],A[R[i]]);
for(int i=1;i<n;i<<=1){
int t0=qm(3,(mod-1)/(i<<1)),x,y;
for(int j=0;j<n;j+=i<<1){
int t=1;
for(int k=0;k<i;k++,t=1ll*t*t0%mod){
x=A[j+k];y=1ll*t*A[j+k+i]%mod;
A[j+k]=(x+y)%mod;A[j+k+i]=(x-y+mod)%mod;
}
}
}
}
inline void mul(int *A,int *B){
NTT(A);NTT(B);
for(int i=0;i<=n;i++)A[i]=1ll*A[i]*B[i]%mod;
NTT(A);
reverse(A+1,A+n);
for(int i=0,t=inv(n);i<=n;i++)A[i]=1ll*A[i]*t%mod;
}
int Fac[N],Finv[N],Gac[N],Ginv[N],a[N],b[N],f[N];
void priwork(int n){
Fac[0]=Finv[0]=Gac[0]=Ginv[0]=1;
for(int i=1;i<=n;i++){
Fac[i]=1ll*Fac[i-1]*i%mod;
Finv[i]=inv(Fac[i]);
Gac[i]=qm(G,1ll*i*i);
Ginv[i]=inv(Gac[i]);
}
}
inline void solve(int l,int r){
if(l==r)return ;
int mid=(l+r)>>1,L;
solve(l,mid);
m=r-l+1;
for(n=1,L=0;n<=m;n<<=1)L++;
for(int i=0;i<n;i++)R[i]=(R[i>>1]>>1)|((i&1)<<(L-1)),a[i]=b[i]=0;
for(int i=l;i<=mid;i++)a[i-l]=f[i];
for(int i=1,o=1?1:-1;i<m;i++,o=-o){
b[i]=1ll*o*Finv[i]*Ginv[i]%mod;
if(b[i]<0)b[i]+=mod;
}
mul(a,b);
for(int i=mid+1;i<=r;i++)f[i]=(f[i]+a[i-l])%mod;
solve(mid+1,r);
}
int main(){
freopen("pp.in","r",stdin);
freopen("pp.out","w",stdout);
int n;cin>>n;
priwork(n);f[0]=1;
solve(0,n);
f[n]=1ll*f[n]*Fac[n]%mod*Gac[n]%mod;
printf("%d\n",f[n]);
return 0;
}
原文:https://www.cnblogs.com/Yuzao/p/8551286.html