第三章 使用sklearn 实现机学习的分类算法
分类算法
- 分类器的性能与计算能力和预测性能很大程度上取决于用于模型训练的数据
- 训练机器学习算法的五个步骤:
- 特征的选择
- 确定评价性能的标准
- 选择分类器及其优化算法
- 对模型性能的评估
- 算法的调优
sklearn初步使用
- 3.1 sklearn中包括的processing 模块中的标准化类,StandardScaler对特征进行标准化处理
from sklearn.processing import StandardSacler
sc=StandardScaler() #实例化
sc.fit(X_train)
sc.transform(X_train)
# - 以上两句可以并写成一句sc.fit_transform(X_trian)
# - 我们使用相同的放缩参数分别对训练和测试数据集以保证他们的值是彼此相当的。**但是在使用fit_transform 只能对训练集使用,而测试机则只使用fit即可。**
# - sklearn中的metrics类中包含了很多的评估参数,其中accuracy_score,
# - 中accuracy_score(y_test,y_pred),也就是那y_test与预测值相比较,得出正确率
y_pred=model.predict(X_test-std)
过拟合现象
过拟合现象出现有两个原因:
- 训练集与测试集特征分布不一致(黑天鹅和白天鹅)
- 模型训练的太过复杂,而样本量不足。
同时针对两个原因而出现的解决方法:
- 收集多样化的样本
- 简化模型
- 交叉检验

逻辑斯谛回归
感知机的一个最大缺点是:在样本不是完全线性可分的情况下,它永远不会收敛。
分类算中的另一个简单高效的方法:logistics regression(分类模型)
- 很多情况下,我们会将逻辑回归的输出映射到二元分类问题的解决方案,需要确保逻辑回归的输出始终落在在0-1之间,此时S型函数的输出值正好满足了这个条件,其中:

几率比(odd ratio)
特定的事件的发生的几率,用数学公式表示为:$\frac{p}{1-p} $,其中p为正事件的概率,不一定是有利的事件,而是我们将要预测的事件。以一个患者患有某种疾病的概率,我们可以将正事件的类标标记为y=1。

- 也就是样本特征与权重的线性组合,其计算公式:
z=w^T
- 预测得到的概率可以通过一个量化器(单位阶跃函数)简单的转化为二元输出
- 如果y>0.5 则判断该样本类别为1,如y<0.5,则判定该样本是其他类别。
- 对应上面的展开式,如果z≥0,则判断类别是1,否则是其他。
- 阈值也就是0.5
通过逻辑斯谛回归模型的代价函数获得权重
- 判定某个样本属于类别1或者0 的条件概率如下:

- 逻辑回回归的代价函数是最小二乘损失函数
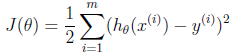
- 为了推导出逻辑斯蒂回归的代价函数,需要先定义一个极大似然函数L,

- 用极大似然估计来根据给定的训练集估计出参数w,对上式两边取对数,化简为

求极大似然函数的最大值等价于求-l(w)的最小值,即:

利用梯度下降法求参数
- 在开始梯度下降之前,sigmoid function有一个很好的性质,

梯度的负方向就是代价函数下降最快的方向,借助泰勒展开,可以得到(函数可微,可导)

其中,f‘(x) 和δ为向量,那么这两者的内积就等于

当θ=π时,也就是在δ的f‘(x)的负方向时,取得最小值, 也就是下降的最快的方向了

也就是

- 其中,wj表示第j个特征的权重,η为学习率,用来控制步长。
- 对损失函数J(θ)中的θ的第j个权重求偏导,

所以,在使用梯度下降法更新权重时,只要根据公式

当样本量极大的时候,每次更新权重需要耗费大量的算力,这时可以采取随机梯度下降法,这时,每次迭代的时候需要将样本重新打乱,然后用下面的式子更新权重

参考文献:
- Raschka S. Python Machine Learning[M]. Packt Publishing, 2015
- 周志华. 机器学习 : = Machine learning[M]. 清华大学出版社, 2016.
逻辑回归推导
原文:https://www.cnblogs.com/onemorepoint/p/9321199.html