现在有一堆数字共N个数字(N<=10^6),以及一个大小为k的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
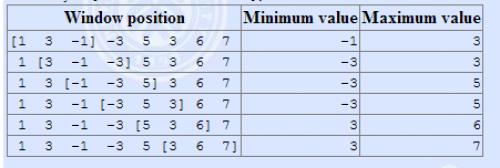
输入格式:
输入一共有两行,第一行为n,k。
第二行为n个数(<INT_MAX).
输出格式:
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
50%的数据,n<=10^5
100%的数据,n<=10^6
一开始写的是线段树,结果WA一个TLE三个,后来换用单调队列成功AC
单调队列中的元素满足单调递增/减(看情况)
对于本题来模拟一下单调队列的工作情况,以求最大值为例
1.设两个数组,p[]是单调队列数组,q[]是保存元素下标的数组
8 3 1 3 -1 -3 5 3 6 7
2.首先,队列为空,1入队,此时p[]={1},q[]={1};
3.轮到3,3>1,那么1就可以出队了,因为只要有3在,在滑动窗口内1永远不会被选为最大值,此时p[]={3},q[]={2};
4.轮到-1,虽然-1<3,但是一旦3离开了窗口,-1还是有可能成为最大值的,所以-1入队,此时p[]={3,-1},q[]={2,3};
5.轮到-3,同4分析,虽然-3<-1,但一但-1出了窗口,-3还是有可能翻身的,所以-3入队,,此时p[]={3,-1,-3},q[]={2,3,4};
6.轮到5,同2分析,只要有5在,-1和-3永远翻不了身,所以-1,-3出队,5入队,此时3已经离开了窗口,所以3也出队
,此时p[]={5},q[]={5};
7.轮到3,同4分析,3还是有机会的,入队,此时p[]={5,3},q[]={5,6};
8.轮到6,同2分析,5和3可以一边凉快去了,5,3出队,6入队,此时p[]={6},q[]={7};
9.轮到7,同2分析,6失败离场,出队,7入队,此时p[]={7},q[]={8};
到此结束,可以发现,队首一定是最大的元素,所以每次输出队首即可
void que_max() { head=1;tail=0;//队尾一定要严格对应队尾元素,所以初始化为0 for(int i=1;i<=n;i++) { while(tail>=head&&a[i]>q[tail])//如果队中有元素且新的元素大于队尾元素 tail--;//队尾元素出队 q[++tail]=a[i];//新的元素入队 p[tail]=i;//保存下标 while(p[head]<=i-k)//如果队首已经离开了窗口 head++;//队首元素出队 if(i>=k)printf("%d ",q[head]);//i>=k输出不解释 } printf("\n"); }
最小值情况同上
完整代码
#include<bits/stdc++.h> using namespace std; const int MAXN=1e6+10; int a[MAXN],head,tail,q[MAXN],p[MAXN],n,k; void que_max() { head=1;tail=0; for(int i=1;i<=n;i++) { while(tail>=head&&a[i]>q[tail]) tail--; q[++tail]=a[i]; p[tail]=i; while(p[head]<=i-k) head++; if(i>=k)printf("%d ",q[head]); } printf("\n"); } void que_min() { head=1;tail=0; for(int i=1;i<=n;i++) { while(tail>=head&&a[i]<q[tail]) tail--; q[++tail]=a[i]; p[tail]=i; while(p[head]<=i-k) head++; if(i>=k)printf("%d ",q[head]); } printf("\n"); } int main() { cin>>n>>k; for(int i=1;i<=n;i++) cin>>a[i]; que_min();que_max(); return 0; }
参考大佬@hankeke的题解
原文:https://www.cnblogs.com/pcpcppc/p/9338862.html