笔记:Neworld2002
整数集合\(Z\){-1,0,1...}
自然数集合\(N\){0,1,2,...}
整除 :若\(a=bk\),三数均为整数,则\(b\)整除\(a\)
约数:若\(b\)整除\(a\),且\(b\geqslant0\),则b是a的约数
1整除任何数,任何数整除0
若a整除b,a整除c,则a整除(b+c),a整数(b-c)
证明:
\(\because a\)整除\(b\),\(a\)整除\(c\),\((a \neq 0)\)
\(\therefore b = an ,c = am\)
\(\therefore (b+c) = an+am = a(n+m)\)
\(\therefore a\)整除\((b+c)\)
同理可证,\(a\)整除\((b-c)\)
若a整除b,则对任何数c,都有a整除(bc)
若a整除b,b整除c,则a整除c
证明:
\(\because a\)整除b,\(b\)整除\(c\)
\(\therefore an = b , bm = c\)
\(\therefore anm = c\)
\(\therefore a\)整除\(c\)
即传递性
因子:对一个正整数a来说,除了1和a本身,其他约数均为它的因子
//c++
inline bool Prime(int n){
if(n==1)return false;
for(register int i=2;i*i<=n;++i){
if(n%i==0)return false;
}
return true;
}// pascal
function prime(n:longint):boolean;
var i:longint;
begin
if(n==1)exit(false);
for i:=2 to trunc(sqrt(n)) do
if(n mod i = 0)exit(false);
exit(true);
end;若整数\(N \geqslant 2\),那么\(N\)一定可以惟一地表示为若干素数的乘积(素因子)。
\[ N = p_1^{r_1} p_2^{r_2}... p_k^{r_k} (p_i为素数,r_i\geqslant 0) \]
18 = 2 * 3 * 3 = 2^1 * 3^2
45 = 3 * 3 * 5
.....
显而易见,对于一个合数N,一定存在两个数,使其相乘为N,这两个数就是N的因子。
若这两个数不为素数,则可以继续将这两个数分解,直至得到素数。
综上所述,一个合数N,是由多个素因子相乘得到。
设\(N = am\),\(a\)和\(m\)都是N的因子,且\(a\)为N的素因子,\(a\)是N最小的素因子
\\c++
std::vector<int> fac(int x){
vector<int>ret;
for(register int i=2;i*i<=x;++i){//循环每个质因数
while(x%i==0){//如果i整除x
ret.push_back(i);//把i放进数组里
x /= i;//除去掉一个i
}
}
if(x>1)ret.push_back(x);
return ret;
}\\pascal 不会写代码思路
不想写pascal……
考虑开一个数组,从小到大枚举x的素因数,然后判断这个数是否整除x,如果整除就把它丢进数组里,并且x div 它,去掉这个数。由于这个数可能出现多次:如4 = 2*2,所以要弄个while循环除以它,直到x不含有这个数
#define MAXN 200005
bool prime[MAXN];
void eratos(int N){
std::memset(prime,true,sizeof(prime));
prime[0] = prime[1] = false;
for(register int i=2;i*i<=N;++i)
if(prime[i]==true){
for(register int j=i*i;j<=N;j+=i)prime[j]=false;
}
}#define MAXN 1000000
bool prime[MAXN];
int Minfac[MAXN];
void init(int n){//初始化
prime[0] = prime[1] = false;//0和1都不是素数
Minfac[0] = Minfac[1] = -1//两数都没有素因子
for(register int i=2;i<=n;++i){
prime[i] = true;
Minfac[i] = i;
}
}void eratos(int n){
for(register int i=2;i*i<=n;++i){
if(prime[i]==true){//如果是质数
for(register int j=i*i;j<=n;j+=i){
prime[j] = false;//将其倍速设为false
if(Minfac[j]==j){//如果之前没有找打这个数的最小素因子
Minfac[j] = i;//i就是它的最小素因子
}
}
}
}
}std::vector<int> factor(int x){
std::vector<int>res;
while(x>1){
ret.push_back(Minfac[x]);//将最小的素因子加入数组
x /= Minfac[x];//除掉它
}
}显而易见埃式筛法会出现一个数被筛多次。
30 = 2·15 = 3·10 = 5·6
30这个数就被2、3、5筛了三次
如果每个合数只被它的最小素因子筛出,那么这个数只被筛一次
时间复杂度可以达到\(O(N)\),是线性的
void Euler_sieve(int n){
std::memset(isprime,true,sizeof(isprime));//初始化所有数都是素数
int tot = 0;//tot记录素数数量
for(register int i=2;i<=n;++i){
if(isprime[i]){//如果这个数是素数
tot += 1;//素数数量+1
prime[tot] = i;//放入素数表内
}
for(register int j=1;j<=tot;++j){//遍历素数表
if(i*prime[j]>n)break;//超过n就没必要继续筛了
isprime[i*prime[j]] = false;//把i*prime[j]筛掉
if(i%prime[j]==0)break;
//当i中含有prime[j]这个素因子时应该停止循环,避免之后出现比prime[j]更大的素因子,使得每个数只被最小素因子筛掉
}
}
}举例:
12的正约数有6个:1、2、3、4、6、12
将12分解素因数得:\(12 = 2^2 · 3^1\)
\((r_1+1)(r_2+1) = (2+1)(1+1) = 6\)
证明如下:
首先同上,n可以分解质因数:\(N = p_1^{r_1}p_2^{r_2}...p_k^{r_k}(p_i为素数,r_i\geq 0)\)
由约数定义可知\(p_1^{r_1}\)的约数有:\(p_1^0 、p_2^1、p_1^3 ... p_1^{r_1}\) ,共(\(r_1+1\))个;同理\(P_2^{r_2}\)的约数有(\(r_2+1\))个......\(p_k^{r_k}\)的约数有(\(r_k+1\))个。
故根据乘法原理:n的约数的个数就是\((r_1+1)(r_2+1)...(r_k+1) = \prod_{i=1}^{k}(r_i+1)\)
——《百度百科》约数个数定理
\(N\)的约数个数上界为\(2\sqrt{N}\)
\(N\)所有的正约数和为:\((1+p_1+p_1^{2}+...+p_1^{r_1})(1+p_2+p_2^{2}+...+p_2^{r_2})...(1+p_k+p_k^{2}+...+p_k^{r_k}) = \prod_{i=1}^{k}(\sum_{j=0}^{r_i}p_i^j)\)
设\(a\)和\(b\)都是不为0的整数,\(c\)为满足整除\(a\)也整除\(b\)的最大整数,则称\(c\)为\(a\)、\(b\)的最大公约数,记为\(gcd(a,b)\)
从\(min(a,b)\)到1枚举\(i\),判断是否能整除两数,如果可以就输出并退出循环
时间复杂度\(O(min(a,b))\)
min(a,b) = a和b的较小值
max(a,b) = a和b的较大值
当\(a = p_1^{r_2}p_2^{r_2}..p_k^{r_k} , b = p_1^{s_1}p_2^{s_2}..p_k^{s_k}\)时,第\(i\)项的\(r_i , s_i \geqslant 0\)
则\(gcd(a,b) = p_1^{min(r_1,s_1)}p_2^{min(r_2,s_2)}...p_k^{min(r_k,s_k)}\)
int gcd(int a,int b){
int ans = 1;
for(register int i=2;i*i<=std::min(a,b);++i){
while(a%i==0&&b%i==0){//当两数均含i这个因子
a/=i;b/=i;ans*=i;//除去这个质因子,并且ans乘上i
}
while(a%i==0)a/=x;//若a还含有i这个因子,应该去干净
while(b%i==0)b/=x;//同上
}
if(a%b==0)ans*=b;//如果b整除a
else if(b%a==0)ans*=a;//如果a整除b
return ans;//ans即为答案
}时间复杂度约为\(O(\sqrt{min(a,b)})\)
自己估计的好像不准
以上两个算法时间慢,还不好写,直接丢弃。
先上代码
int gcd(int a,intb){
if(b==0)return a;
else return gcd(b,a%b);
}没错,写完了。
当然在C++里还可以写得更短
int gcd(int a,int b){return b==0 ? a : gcd(b,a%b);}时间复杂度为\(O(log(a+b))\),不管在效率还是代码量方面都碾压上述算法
该算法也叫辗转相除法
根据上面的代码,我们会发现是基于\(gcd(a,b) = gcd(b,a\bmod b)\)
求证:\(gcd(a,b) = gcd(b,a\bmod b)\)
证明如下:
设\(d\)为\(a\)和\(b\)的任意公约数,则有\(a = ld,b = md\)
\(\because a\geqslant b\)
\(\therefore b\)可以通过一次乘法和一次加法后得到\(a\)
\(\therefore a = bq+r (a \geqslant b)\)
将\(a = ld,b = md\)代入
得\(ld = mdq + r\)
移项得\(r = ld - mdq = d(l-mq)\)
则\(d\)为\(r\)的约数
\(\because a = bq+r\)
\(\therefore a \bmod b = r\)
又\(d\)为\(a,b\)的任意公约数
综上所述,得:\(a,b\)的任意公约数,也都是\(a \bmod b\)的约数
\(\therefore gcd(a,b) = gcd(b,a \bmod b)\)
这道题直接用GCD是不行的,显而易见是道高精题,但不过高精模可能比较尴尬,我不会写
所以需要引入一些改进——适用于高精度数的二进制法
\(a<b\)时,\(gcd(a,b) = gcd(b,a)\)
\(a = b\)时,\(gcd(a,b) = a\)
\(a,b\)均为偶数时,\(gcd(a,b) = 2*gcd(a/2,b/2)\)
\(b\)为偶数\(a\)为奇数时,则\(a\)中必无2这个因子,所以\(gcd(a,b) = gcd(a,b/2)\)
若两数都是奇数,\(gcd(a,b) = gcd(b,a-b)\),这步也叫更相减损术,出自《九章算术》
代码实现时切记传参传数组。
\[ |A| = \lfloor \frac{600}{2} \rfloor = 300, |B| = \lfloor \frac{600}{3} \rfloor = 200,|C| = \lfloor \frac{600}{5} \rfloor = 120 \]
\[ |A \cap B| = \lfloor \frac{600}{2*3}\rfloor = 100,|A \cap C| = \lfloor \frac{600}{2*5}\rfloor = 60,|B \cap C| = \lfloor \frac{600}{3*5}\rfloor = 40 \]
\[ |A \cap B \cap C| = \lfloor \frac{600}{2*3*5}\rfloor = 20 \]
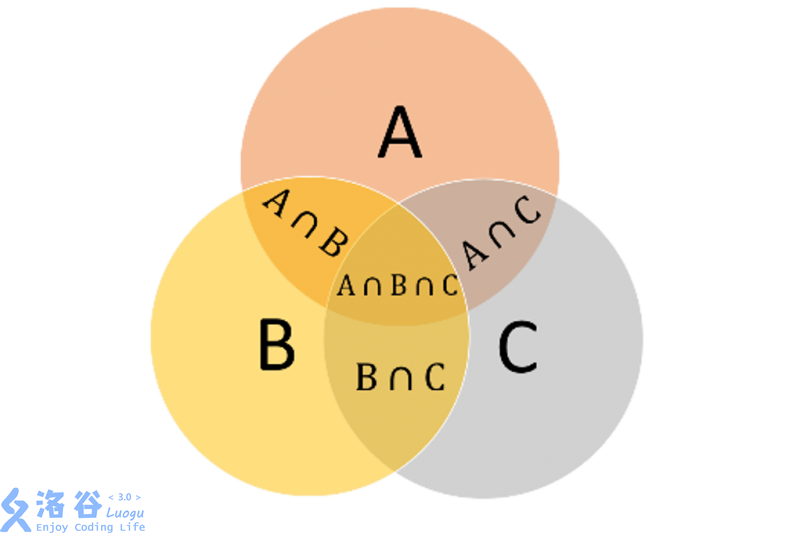
\(\varphi(8) = 4\)
小于8且与8互素的数是1,3,5,7
若将\(N\)分解为不同素数的乘积,即:
\(N = p_1^{r_1}p_2^{r_2}...p_k^{r_k}\)
设1到\(N\)中的数,为\(p_i\)的倍数的集合为\(A_i\),$|A_i| = \lfloor \frac{N}{p_i}\rfloor(i=1,2,..,k) $
对于$p_i \neq p_j,A_i \cap A_j \(即是\)p_i\(和\)p_j$的公倍数,即
\(|A_i \cap A_j| = \lfloor \frac{N}{p_ip_j}\rfloor(1 \leq i,j \leq k,i \neq j)\)
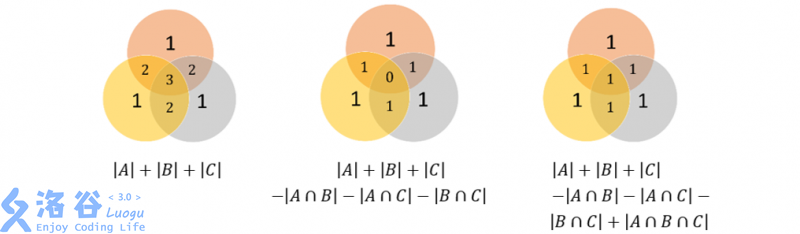
在取出\(|A_i||A_j|\)时,\(p_i,p_j\)的公倍数被去除了两次,所以要加回来
\[
\varphi(N) = N - (\frac{N}{p_1}+\frac{N}{p_2}+...+\frac{N}{p_k}) + (\frac{N}{p_1p_2}+\frac{N}{p_2p_3}+...+\frac{N}{p_1p_k}) \pm (\frac{N}{p_1p_2..p_k})
\]
\[ \varphi(N) = N(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_k}) \]
int euler_phi(int n){
int res = n;
for(register int i=2;i*i<=n;++i){
if(n%i==0){
res = res / i * (i-1);
for(;n%i==0;n/=i);
}
}
if(n!=1)res = res / n * (n-1);
return res;
}时间复杂度为\(O(\sqrt{N})\)
int euler[MAXN];
void euler_phi(){
for(register int i=0;i<MAXN;++i)euler[i] = i;
for(register int i=2;i<MAXN;++i){
if(euler[i]==i){
for(register int j=i;j<MAXN;j+=i)
euler[j] = euler[j] / i * (i-1);
}
}
}筛出一个欧拉函数表
证明:
\(\because gcd(a,m) = gcd(m,a\bmod m),gcd(b,m) = gcd(m,b\bmod m)\)
又\(a \bmod m = b \bmod m\)
\(\therefore gcd(a,m) = gcd(b,m)(a \equiv b \pmod m)\)
#### 定义
设\(b = q*\varphi(m) + r\),其中\(0 \leq r \leq \varphi(m)\),即\(r = b \bmod \varphi(m)\)
则$a^b \equiv a^{q\varphi(m)+r} \equiv (a^{\varphi(m)})^qa^r \equiv 1^q*a^r \equiv a^r \equiv a^{b \bmod \varphi(m)}\pmod m $
已知整数a与整数p互质,即gcd(a,p)=1,定义关于x的方程,称x为a关于模p的逆元
\[
ax \equiv 1 \pmod p
\]
我们需要特别注意,当两数不是互质时,没有逆元
通常情况下,有些题目会要求我们MOD一个数,我们可以通过同余定理来计算
但是需要特别注意,如下式
\[
(a/b) \bmod p
\]
不可以写成
\[
(a \bmod p) / (b \bmod p)\bmod p
\]
但可以写成其中b^-1是a关于模p的逆元
假如a是整数,p是质数,则a,p显然互质(即两者只有一个公约数,那么我们可以得到费马小定理的一个特例,即当p为质数时候, a^(p-1)≡1(mod p)
如上,我们需要特别注意,只能当p为质数时,才能使用费马小定理求解逆元
\[
a^{p-1}\equiv 1 \pmod p
\]
\[ a*a^{p-2}\equiv1 \pmod p \]
则可知,a^(p-2)为a关于模p的逆元,此时只需要快速幂求解即可
费马小定理求逆元的时间复杂度是O(logN),但常数较大
#include <cstdio>
#define MAXN 3000005
long long N,P;
long long inv[MAXN];
int main(){
scanf("%lld%lld",&N,&P);
inv[1] = 1;
puts("1");
for(register int i=2;i<=N;++i){
inv[i] = (P-(P/i))*(inv[P%i])%P;
printf("%lld\n",inv[i]);
}
return 0;
}当\(b = 0\)时,\(gcd(a,b) = a\)。则\(x = 1,y = 0\)
当\(ab \neq 0\)时,设\(ax_1 +by_1 = gcd(a,b),bx_2 + (a \bmod b)y_2 =gcd(b,a\bmod b)\)
根据朴素的欧几里得原理有\(gcd(a,b) = gcd(b,a\bmod b)\)
则:\(ax_1 + by_1 = bx_2 + (a \bmod b)y_2\)
即:\(ax_1 +by_1 = bx_2 + (a -(a/b)*b)y_2 = bx_2 + ay_2 - (a/b)*by_2 = ay_2 - b((a/b)y_2-x_2)\)
得:\(x_1 = y_2,y_1 = x_2 - (a/b)y_2\)
int x,y;
int exgcd(int a,int b,int &x,int &y){
if(b==0){x=1;y=0;return a};
int d = exgcd(b,a%b,y,x);
y = y -a/b*x;
return d;
}求解不定方程
求解线性方程(同余方程)与逆元
若\(ax \equiv 1 \pmod p\),且\(gcd(a,p)=1\)
则有:\(ax + py = 1\),且\(x\)为\(a\)的逆元
原文:https://www.cnblogs.com/Neworld2002/p/9350906.html