我学的时候看的是yyb的博客
1.KMP字符串匹配
2.trie树
要求入门并能有一定技巧地运用
(匹配泛指各种字符串之间相互包含,交集等问题)
我们学习了KMP,是用来2个字符串匹配的算法:O(m+n)
现在给出很多个字符串,去把他们和另外一个字符串匹配,如果逐个匹配,显然会很慢,所以引入一种新算法:AC自动机
- Q:多个字符串?
A:我们学了trie树是吧,预备一下,全丢进去- Q:字符串匹配?
A:我们学了KMP对吧,想一下KMP的原理,突然发现next[]是不是很吊,预备一下,肯定有用,但是肯定预处理方法不同(见后)- Q:这个我也想得到啊!
A:所以肯定是一个KMP结合trie树的算法,它就叫AC自动机
注意:以luogu AC自动机模板为例
首先一个图,自己画下来再根据代码模拟手玩更容易理解
来自yyb: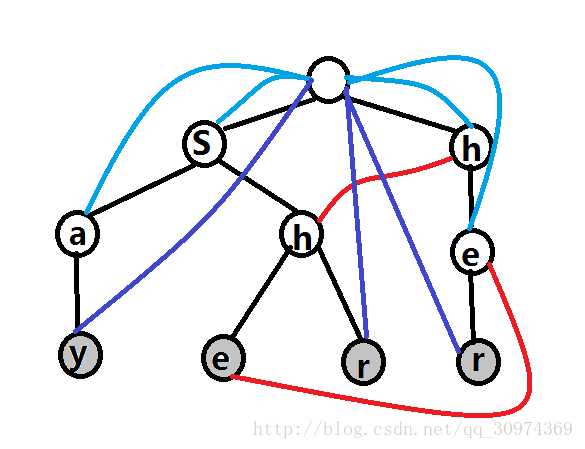
开始!!!
一. 先把所有的匹配字符串丢进trie树,这个不用多说
ljl[].son[]表示now的每一个儿子(26个字母) 板子
ljl[].end记录trie树上在这里结束的是哪个串
PS:代码里trie数组变成了我自己的名字//滑稽,ljl.son[]==trie[][];
il void Insert()
{
rg int len=s.length();
rg int now=0;
for(rg int i=0;i<len;++i)
{
rg int kk=s[i]-‘a‘;
if(!ljl[now].son[kk])
ljl[now].son[kk]=++cnt;
now=ljl[now].son[kk];
}
ljl[now].end++;
}
二.对于匹配,我们考虑找到KMP算法中的next[]数组,但是我们这里把它叫做ljl[].fail,并且也有很多不一样的地方
声明一下:fail指的是当前找到的串(在trie树上找)的最长后缀在哪个地方
PS:根据那个图来找,自己试试
总结一下几个地方(现在大可不必理解,背下来先)
- trie树上第二层所有的fail都是根节点(0),因为最长后缀肯定没有地方可以找到,只能是‘空’
- 我的儿子的fail 是 我的fail的对应儿子(在图上看一下对不对)
- 如果没有想要的儿子,就把我的这个儿子指向我的fail的对应儿子(看后面的板子来理解这句话吧//苦笑)
- 运用类似bfs的方法来找fail
il void get_fail()
{
queue<int> Q;
while(!Q.empty())Q.pop();
for(rg int i=0;i<26;++i)
{
if(ljl[0].son[i])
{
ljl[ljl[0].son[i]].fail=0;//1
Q.push(ljl[0].son[i]);
}
}
while(!Q.empty())
{
rg int now=Q.front();Q.pop();
for(rg int i=0;i<26;++i)
{
if(ljl[now].son[i])
{
ljl[ljl[now].son[i]].fail=ljl[ljl[now].fail].son[i];//2
Q.push(ljl[now].son[i]);
}
else ljl[now].son[i]=ljl[ljl[now].fail].son[i]; //3
}
}
}肯定还是无法理解对不对,接下来还有无法理解的东西,我的建议是先记下来板子,敲板子的时候会有惊喜的!!!(我就是这样理解的)
三.Query匹配暴力跳fail:
每匹配一个新的字母,我们暴力跳一遍它所有的fail(先别质疑复杂度),自己模拟一下,知道正确性就ok了
il int Query(string s)
{
rg int L=s.length();
int now=0,ans=0;
for(rg int i=0;i<L;++i)
{
rg int kk=s[i]-‘a‘;
now=ljl[now].son[kk];//新匹配一个字母
for(rg int tt=now;tt&&ljl[tt].end!=-1;tt=ljl[tt].fail)
//暴力跳fail
{
ans+=ljl[tt].end;
ljl[tt].end=-1;//标记走过!
}
}
return ans;
}嗯,这个应该是分界线吧//滑稽
如果你已经比较理解了或者你有强大的自信心,就往后看,否则,先过了那个板子再说吧……
真的,后面的东西要先理解如何跳fail,我还真不好解释,所以只能自己去理解
好吧,入正题:
这里以
你会发现暴力跳fail会被卡成O(n^2),所以考虑优化(会快很多!)
嗯,以下几点:
- 对于所有的i,从fail[i]向i连边,会构成一棵树
- 既然我们每次要暴跳一遍,为何不做一次跳?
- 那么我们考虑把串T在trie树上标记一下那些单词可以找到
原文:https://www.cnblogs.com/cjoierljl/p/9365569.html