一、逆元
递推逆元
这是别人博客上的证明,来源于:https://blog.csdn.net/rain722/article/details/53170288。
下面是ACdreamers关于递推求解逆元的推导过程(个人觉得他的更好)
其实有些题需要用到


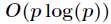
如果对于一个1000000级别的素数
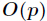
它的推导过程如下,设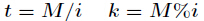
对上式两边同时除
再把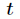
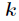
初始化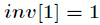


另外


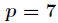
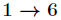
由此,线性筛逆元的代码诞生了:(洛谷3811 AC)
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> using namespace std; long long inv[3000004],n,modd; void dt() { inv[1]=1; for(long long i=2;i<=n;i++) inv[i]=((-(modd/i)*inv[modd%i])%modd+modd)%modd; } int main() { scanf("%lld%lld",&n,&modd); dt(); for(long long i=1;i<=n;i++)printf("%lld\n",inv[i]); return 0; }
二、卡特兰数
1.简介
卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学中一个常出现在各种计数问题中出现的数列。以比
利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名,其前几项为 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862,
16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190,
6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ... ————度
娘
应用:
洛谷1044 栈
#include<iostream> #include<cstring> #include<algorithm> #include<cstdio> using namespace std; long long ans[20]; int n; void catelanshu(int n) { long long a=0; for(int i=0;i<=n-1;i++) { a=a+ans[i]*ans[n-1-i]; } ans[n]=a; } int main() { ans[0]=1;ans[1]=1; cin>>n; for(int i=2;i<=n;i++)catelanshu(i); cout<<ans[n]; return 0; }
原文:https://www.cnblogs.com/czktransformers/p/9366028.html