打眼一看就是最小生成树嘛,但经过板子wa掉的经历后得知,,emmmm,原来是,
构造!
(虽然不知是什么但觉得听起来很厉害的样子...手动微笑)
n=2的情况 自然就是g(1,2)
n=3的情况,由于所有点均为叶子节点,运用树的性质,蓝线部分的 len=(g(1,3)+g(2,3)-g(1,2)) / 2
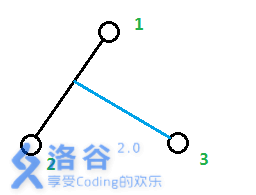
n>3的情况也同理,枚举i看点n是不是从1~i的路径上分叉出来的,求出最小的len加入答案即可
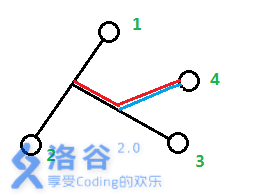
若认为点4是从1~2的路径上分叉出来的,答案就会加上红色部分长度。但是红色部分长度有一部分多余,只有点4是从1~3路径上分叉出来的,才能加上正确答案(蓝色部分)
(洛谷的水印似乎暴露了些什么,消不掉我也很无奈....)
构造好题

#pragma GCC optimize(3) #include<bits/stdc++.h> using namespace std; const int maxn=30; const int INF=(1<<30); int d[maxn][maxn]; int main() { int n; while(scanf("%d",&n)==1&&n) { for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) scanf("%d",&d[i][j]),d[j][i]=d[i][j]; int ans=d[1][2]; for(int i=3;i<=n;i++){ int t=INF; for(int j=2;j<i;j++) t=min(t,(d[1][i]+d[j][i]-d[1][j])/2); ans+=t; } printf("%d\n",ans); } return 0; }
以上
原文:https://www.cnblogs.com/asdic/p/9370156.html