在二分类问题中,假设现在我们有线性可分的训练集\(\mathcal D\)
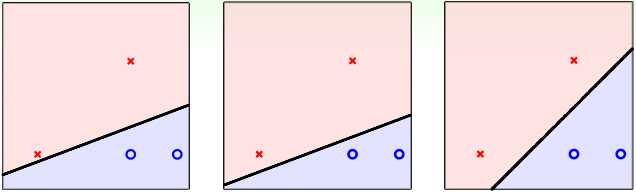
在PLA/口袋算法中,对于上图中的三种假设函数\(h=\mathrm{sign}(w^Tx)\)而言,哪一种是最好的呢?
实际上这三种假设函数对于PLA/口袋算法而言是一样好的,因为它们都满足\(E_{in}(h)=0\),在这个训练集上跑PLA,这三种假设函数最终都有可能得到
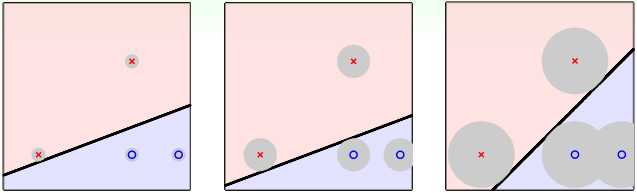
但是如果我们把测试数据的x看作是某个训练样本的\(x^{(i)}\)加上噪声的结果,即测试数据的x在某个训练样本的\(x^{(i)}\)附近(以\(x^{(i)}\)为中心的圆区域内),那么我们希望最终得到的决策边界距离每个训练样本的\(x^{(i)}\)越远越好,这样才能让假设函数对测试数据的噪声(偏差)的容忍度(即上图灰色圆区域半径)尽可能大,因此,我们最希望得到的假设函数应该是上图的第三个。
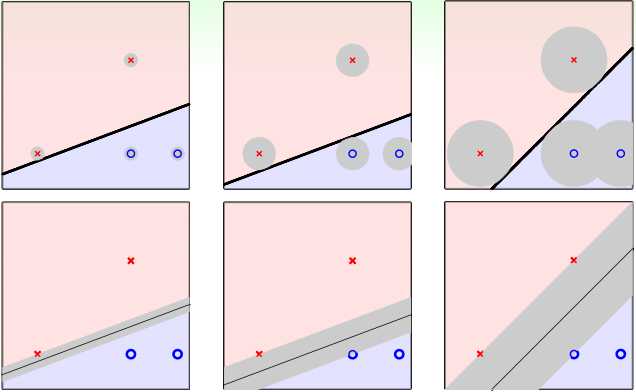
我们把距离决策边界最近的训练样本的\(x^{(i)}\)到边界的距离称为margin,那么我们希望得到margin最大,且\(E_{in}=0\)(即所有的\(y^{(i)}w^Tx^{(i)}>0\))的假设函数,优化目标可以表示为:
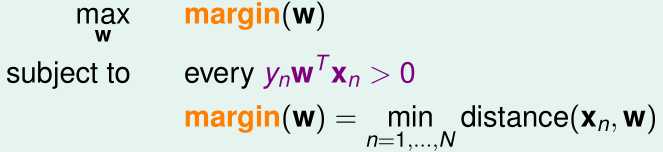
机器学习技法(林轩田)学习笔记:Lecture 1 & Lecture 2
原文:https://www.cnblogs.com/qpswwww/p/9372106.html