目录

• 入门级
  • 引入
  • 正题
• 待更

入门级

引入

先看一道模板题洛谷P3374
题意是:维护一个序列，要求支持两种操作:

1. 把元素\(x\)的值修改成\(y\)
2. 查询区间\([x,y]\)的和
   依然可以用暴力，时间复杂度\(O(n^2)\)，太慢了，出题人不会那么善意的让暴力过掉的
   那么，我们需要优化到\(O(nlog(n))\)，才能过
   看过线段树的同学肯定一下看出来可以用线段树做，但是，线段树的常数比较大，
   一些比较恶意的出题人依然会把它卡掉，所以我们需要常数更小的做法

我们先不考虑修改操作，先考虑查询操作
因为我们查询的是和，我们就可以先预处理出前缀和，然后\(O(1)\)查询
这时候我们再来考虑修改操作
然后我们就要用到树状数组了

正题

1. lowbit函数

这个函数非常重要，它几乎贯彻整个树状数组

int lowbit(int x){
    return x&(-x);
}

\(lowbit(x)=2^{x在二进制下从右往左数第一个1的位置-1}\)
比如\(5_{(10)}=101_{(2)}\)那么\(lowbit(5)=1_{(2)}=1_{(10)}\)
\(~~~~~~~6_{(10)}=110_{(2)}\)那么\(lowbit(6)=10_{(2)}=2_{(10)}\)

2. 树状数组的结构

树状数组算是树型结构了，但在代码中是以数组的形式体现
大小为\(8\)树状数组长这个样子(红色的是边)

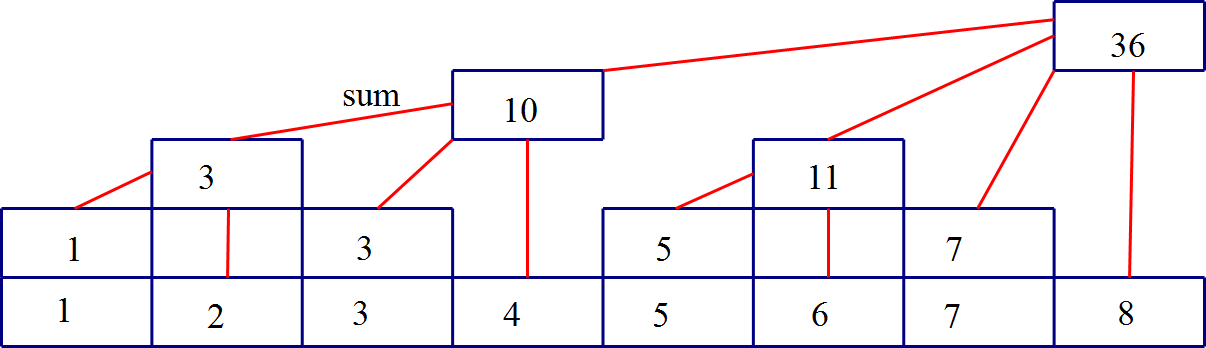
不难看出第\(i\)号节点的父亲是第\(i+lowbit(i)\)号节点
树状数组的第\(x个节点\)表示的是\(\Sigma_{i=x-lowbit(x)+1}^{x}a[i]\)
乍一看好像没什么用，还很复杂，事实上是非常好用的东西

3. 树状数组的修改

树状数组不支持区间修改，只支持单点修改
要修改一个点的值之后，还需要把它到根的路径上的点进行维护
时间复杂度\(O(log(n))\)

void update(int x,int y){//把第x个元素加y
    while(x<=n){
        sum[x]=sum[x]+y;
        x=x+lowbit(x);
    }
}

4. 树状数组的查询

树状数组不支持任意区间查询，只支持查询前缀
但是查询到前缀后，我们就可以得出答案
依然是巧妙的使用\(lowbit\)函数
时间复杂度\(O(log(n))\)

void get_sum(int x){//查询1到x的和
    int re=0;
    while(x){
        re=re+sum[x];
        x=x-lowbit(x);
    }
}

于是我们就把模板题做出来了：

#include<bits/stdc++.h>

using namespace std;

const int MAXN=500001;

int n,m,x,y,t,sum[MAXN];

int lowbit(int x){
    return x&(-x);
}

void update(int x,int y){//把第x个元素加y
    while(x<=n){
        sum[x]=sum[x]+y;
        x=x+lowbit(x);
    }
}

int get_sum(int x){//查询1到x的和
    int re=0;
    while(x){
        re=re+sum[x];
        x=x-lowbit(x);
    }
    return re;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&x);
        update(i,x);
    }
    while(m--){
        scanf("%d",&t);
        if(t==1){
            scanf("%d%d",&x,&y);
            update(x,y);
        }else{
            scanf("%d%d",&x,&y);
            printf("%d\n",get_sum(y)-get_sum(x-1));
        }
    }
}

待更

【树状数组详解】从入门到各种实用技巧

原文：https://www.cnblogs.com/2016gdgzoi316/p/9386124.html