主讲:庄老师
数据处理利器—— Numpy 简介
优点
运算快
封装好
数据存储
可存储为一维数组、二维数组、多维数组
Numpy, Pandas, Scipy 的比较
Numpy 主要以数值矩阵计算为主
Pandas 基于 Numpy 的工具库,常常用于表格数据处理,用来做数据分析
Sci 也是基于 Numpy 的工具库
python 科学计算进阶图

Numpy 详解
属性

数据类型 dtype:
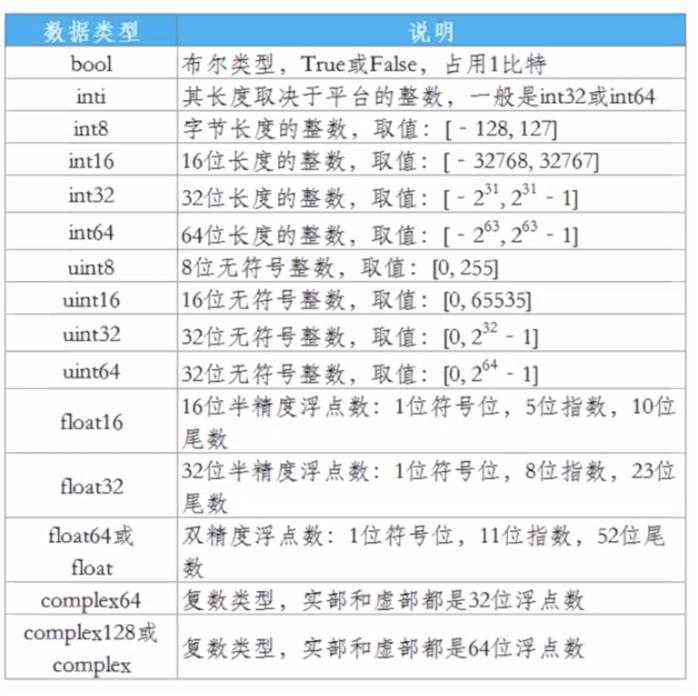
数据类型之间的换算规律:

创建特定的数组:

代码实现:
# 产生 0 填充矩阵
np.zeros(shape, dtype=float, order=‘C‘)
e.g. np.zeros((row , cul))
# 定义一个直线型数组
a.linspaces()
方法一:转换到和目标矩阵一样的shape
np.tranpose(另一个矩阵的形状)
方法二:使用reshape
注意 reshape 中“-1”的使用:
>>> a = np.array([[1,2,3], [4,5,6]])
>>> np.reshape(a, (3,-1)) # the unspecified value is inferred to be 2
array([[1, 2],
[3, 4],
[5, 6]])
-1表示我懒得计算该填什么数字,由python通过a和其他的值3推测出来。# 下面是两张2*3大小的照片(不知道有几张照片用-1代替),如何把所有二维照片给摊平成一维
>>> image = np.array([[[1,2,3], [4,5,6]], [[1,1,1], [1,1,1]]])
>>> image.shape(2, 2, 3)
>>> image.reshape((-1, 6))
array([[1, 2, 3, 4, 5, 6],[1, 1, 1, 1, 1, 1]])
维度与轴:
通过 参数 axis 指定数组对应操作的轴,axis参数的用法如下
axis=0 ,沿着纵轴进行操作
axis=1,沿着横轴进行操作
合并与拆分:
合并:
c1 = np.vstack((a, b)) # 垂直方向上得合并 a 和 b,v 表示 vertical,意思是“垂直的"
c2 = np.hstack((a, a)) # 水平方向上合并 a 和 a
c3 = np.concatenate((a, b), axis=0) # 在垂直方向上合并 a 和 b
拆分:

索引和切片:
索引:
索引数组指定位置的元素: a[m, n]
切片:
对指定维度进行切片: a[m, :],a[:, n]
指定任意范围进行切片: a[m:n, p:q]
基本数学运算与基本函数:
基本数学运算:

基本函数:


广播(broadcasting)
在进行数组之间元素时,会自动检测数组的形状大小,如果不一致,则会通过尾部对齐并扩展数组的方式实现计算
e.g.

生成随机数
导入库:import np.random
生成随机种子:np.random.seed(n)
生成特定分布的随机数:

还有个人平常使用的一些方法:
np.random.randn(row, cul) # 是从标准正态分布中返回一个或多个样本值。
np.random.rand(row, cul) # 随机样本位于[0, 1)中。
数据的存取

python 绘图神器 matplotlib
基本步骤:
1. 导入绘图模块:
import matplotlib.pyplot as plt
2. 绘制图像:
plt.plot()
3. 显示图像:
plt.show()
常用的颜色与线条控制:

标注:

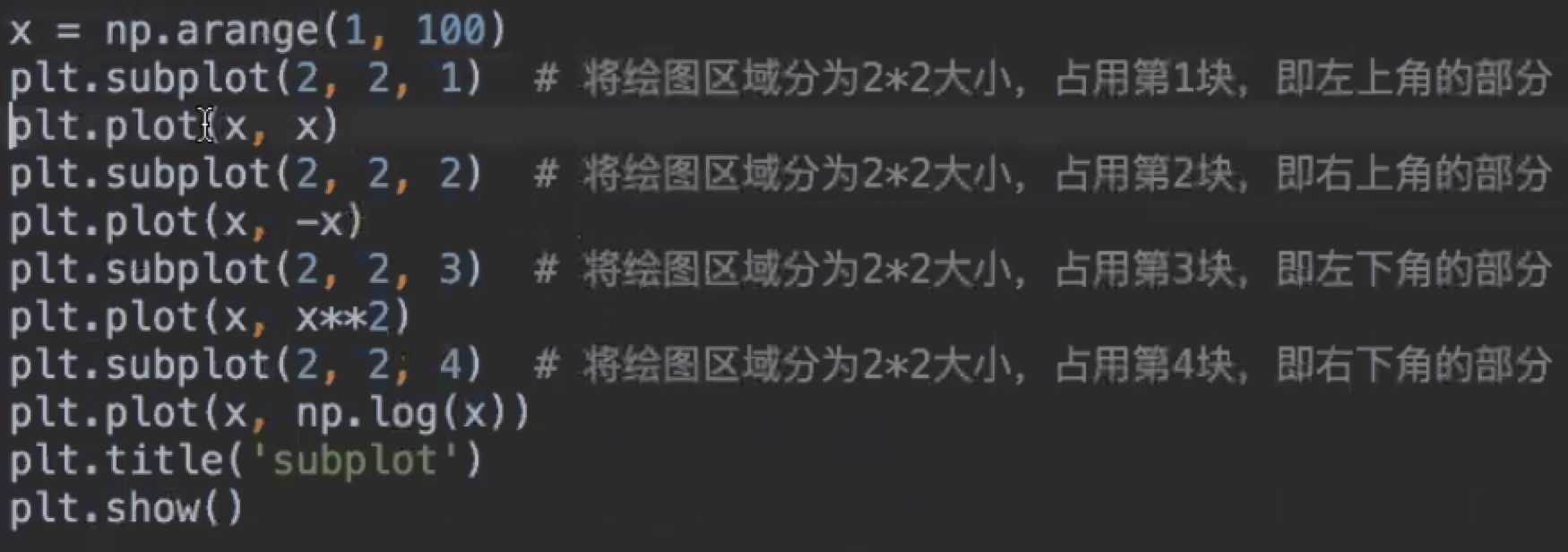
绘制子图:
plt.subplot()
代码实现:
直方图:
plt.hist()
代码实现:

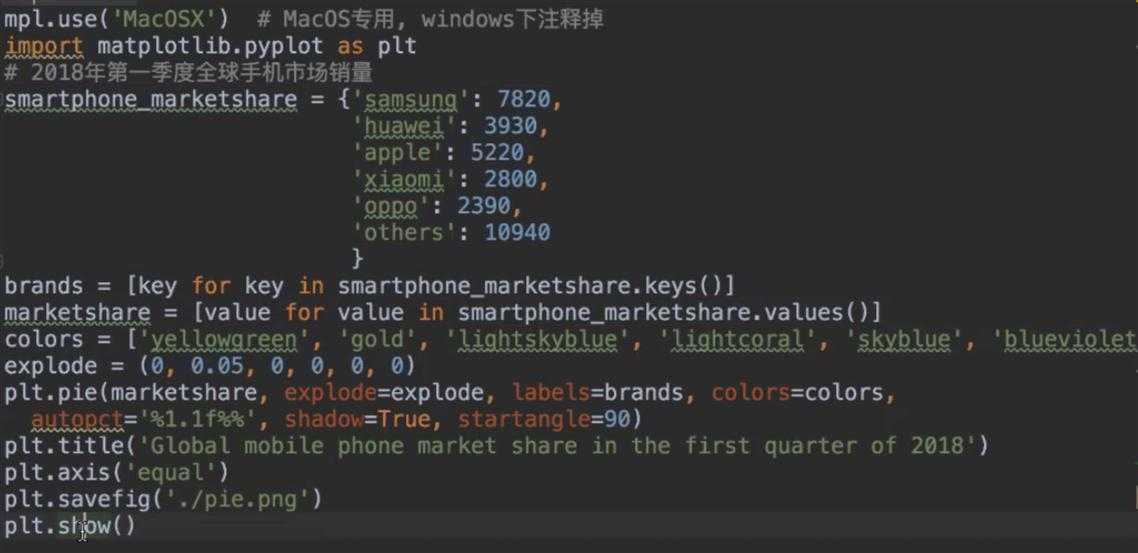
饼状图:
plt.pie()
代码实现一个关于各产商手机销量的饼状图:
Numpy 处理图片
import matplotlib.image as mpimg
代码实现:
读取图片:
img = mpimg.imread(‘*.jpeg‘)
查看图片的形状:
img.shape
显示图像:
plt.imshow(img)
plt.show()
对图像进行切片:
img_part = img[150:600, 250:800, :]
img_ par = img[150:600, 250:800, 0] # 只保存一个红色通道的图片,即是灰度图
利用数组的合并为拼接图片:
img_contact = np.concatenate((img, img), axis=0)
显示图像的部分通道:
r, g, b = np.split(img, 3, axis=2) # 从维度2将图像拆分成3个
交换 b 和 g 通道:
rbg = np.concatenate((r, b, g), axis=2)
原文:https://www.cnblogs.com/Bw98blogs/p/9420451.html