目录
4.1 数据清洗
4.1.1 缺失值处理
4.1.2 异常值处理
4.2 数据集成
4.2.1 实体识别
4.2.2 冗余属性识别
4.3 数据变换
4.3.1 简单函数变换
4.3.2 规范化
4.3.3 连续属性离散化
4.3.4 属性构造
4.3.5 小波变换
4.4 数据规约
4..4.1 属性规约
4.4.2 数值规约
1、常用的数据插补方法
| 均值/中位数/众数插补 | 根据属性值的类型,用该属性取值的均值/中位数/众数进行插补 |
| 使用固定值插补 | 将缺失的属性值用一个常量替换 |
| 最近临插补 | 在记录中找到与缺失样本数据最接近的样本的该属性值插补 |
| 回归方法 | 对带有缺失值的变量,根据已有数据和与其有关的其他变量(因变量)的数据建立拟合模型来预测缺失的属性值 |
| 插值法 | 利用已知点建立合适的插值函数f(x),未知值由对应点 xi 求出的函数值f ( xi )近似代替 |
插值方法:拉格朗日插值法、牛顿插值法、Hermite插值、分段插值、样条插值法等。
拉格朗日插值法利用Python实现:
import pandas as pd from scipy.interpolate import lagrange data=pd.read_excel(r‘E:\siren\Python dataAnalyst\chapter4\demo\data\catering_sale.xls‘) # 过滤异常值,将其变为空值 data[‘销量‘][(data[‘销量‘]<400)|(data[‘销量‘]>5000)]=None #自定义列向量插值函数 def ployinterp_column(s,n,k=5): y=s[list(range(n-k,n))+list(range(n+1,n+1+k))] #取数 y=y[y.notnull()] #剔除空值 return lagrange(y.index,list(y))(n) #插值并返回插值结果 #逐个元素判断是否需要插值 for i in data.columns: for j in range(len(data)): if (data[i].isnull())[j]: #如果为空即插值 data[i][j]=ployinterp_column(data[i],j)
| 异常值处理方法 | 方法描述 |
| 删除含有异常值的记录 | 直接将含有异常值的记录删除 |
| 视为缺失值 | 将异常值视为缺失值,利用缺失值处理的方法进行处理 |
| 平均值修正 | 可用前后两个观测值的平均值修正改异常值 |
| 不处理 | 直接在具有异常值的数据集上进行挖掘 |
在很多情况下,要先分析异常值出现的可能原因,在判断异常值是否应该舍弃,如果是正确数据,可直接在具有异常值的数据集上进行挖掘建模。
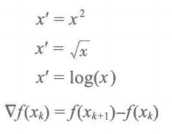
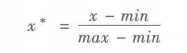
离差标准化保留了原来数据中存在的关系,是消除量纲和数据取值范围影响的最简单方法。
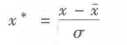
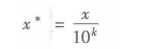
1 1 data=pd.read_excel(r‘E:\siren\Python dataAnalyst\chapter4\demo\data\normalization_data.xls‘) 2 2 #标准差标准化 3 3 (data-data.mean())/data.std() 4 4 5 5 #最小-最大规范化 6 6 (data-data.min())/(data.max()-data.min()) 7 7 8 8 #小数定标规范化 9 9 data/10**np.ceil(np.log10(data.abs().max())
1 import pandas as pd 2 3 data = pd.read_excel(r‘E:\siren\Python dataAnalyst\chapter4\demo\data\discretization_data.xls‘) #读取数据 4 data = data[u‘肝气郁结证型系数‘].copy() 5 k = 4 6 7 d1 = pd.cut(data, k, labels = range(k)) #等宽离散化,各个类比依次命名为0,1,2,3 8 9 #等频率离散化 10 w = [1.0*i/k for i in range(k+1)] 11 w = data.describe(percentiles = w)[4:4+k+1] #使用describe函数自动计算分位数 12 w[0] = w[0]*(1-1e-10) 13 d2 = pd.cut(data, w, labels = range(k)) 14 15 from sklearn.cluster import KMeans #引入KMeans 16 kmodel = KMeans(n_clusters = k, n_jobs = 4) #建立模型,n_jobs是并行数,一般等于CPU数较好 17 kmodel.fit(data.reshape((len(data), 1))) #训练模型 18 c = pd.DataFrame(kmodel.cluster_centers_).sort(0) #输出聚类中心,并且排序(默认是随机序的) 19 w = pd.rolling_mean(c, 2).iloc[1:] #相邻两项求中点,作为边界点 20 w = [0] + list(w[0]) + [data.max()] #把首末边界点加上 21 d3 = pd.cut(data, w, labels = range(k)) 22 23 def cluster_plot(d, k): #自定义作图函数来显示聚类结果 24 import matplotlib.pyplot as plt 25 plt.rcParams[‘font.sans-serif‘] = [‘SimHei‘] #用来正常显示中文标签 26 plt.rcParams[‘axes.unicode_minus‘] = False #用来正常显示负号 27 28 plt.figure(figsize = (8, 3)) 29 for j in range(0, k): 30 plt.plot(data[d==j], [j for i in d[d==j]], ‘o‘) 31 32 plt.ylim(-0.5, k-0.5) 33 return plt 34 35 cluster_plot(d1, k).show() 36 37 cluster_plot(d2, k).show() 38 cluster_plot(d3, k).show()

原文:https://www.cnblogs.com/dataAnalysis/p/9413686.html