题目大意:
输入t,t个测试用例
每个测试用例输入n
接下来n行 输入u,v,w,树的无向边u点到v点权重为w
求任意两点间的最大流的总和
1.最大流最小割定理 即最大流等于最小割
2.无向树上的任意两点都可互达 也就是说 源点S可经其他任何点流到汇点T
设dist(x , y) 为在树上 x 到 y 的距离
由2能知道,S的总流量就是 n∑i=1 dis( s , i )
然后就是题解上的 S到其他各个点的距离 和 T到其他各个点的距离 中较小的即为最小割

举个栗子
4
1 2 3
1 3 4
3 4 5
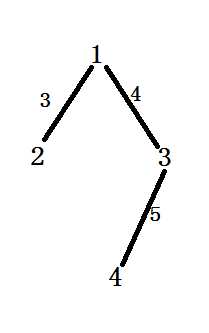
通过树形DP
ll dis[MAXN], son[MAXN], dp[MAXN]; /// dis[ i ]为从 i 点向下的分支的长度总和 /// son[ i ]为从 i 点向下的总点数(包括它本身) /// dp[ i ]为从 i 点出发去其他所有点的长度总和 void dfs1(ll u,ll f) /// 求dis[],son[] { son[u]=1; for(int i=0;i<vec[u].size();i++) { ll v=vec[u][i].F, w=vec[u][i].S; if(v==f) continue; dfs1(v,u); son[u]+=son[v]; dis[u]+=dis[v]+son[v]*w; } } void dfs2(int u,int f) /// 通过dis[]进行树形DP { for(int i=0;i<vec[u].size();i++) { ll v=vec[u][i].F, w=vec[u][i].S; if(v==f) continue; dp[v]=dp[u]+(n-2*son[v])*w; dfs2(v,u); } } ...... dfs1(1,0); dp[1]=dis[1]; dfs2(1,0); ......
/*结果为
dis[] 16 0 5 0
son[] 4 1 2 1
dp[] 16 22 16 26
*/
可以转化为一个(姑且称之为)流量图
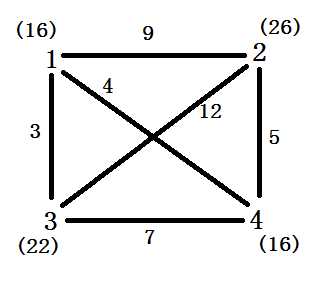
括号内的是到该点的总流量
那么 S到T的最大流 就是 两者总流量中 小的一个
sort(dp+1,dp+1+n); __int128 ans=0; for(int i=1;i<n;i++) ans += dp[i]*(n-i);
当某个点x的总流量是所有点中的最小值时
那么x与其他所有点的最大流就是x的总流量
所以这里可以直接贪心 排序一下
第 i 个点与后面比它(的总流量)小的所有点(n - i 个)直接取第 i 个
也可以不用 __int128 ,开个数组模拟一下
int ans[105]; memset(ans,0,sizeof(ans)); for(ll i=1;i<n;i++) { ans[0] += dp[i]*(n-i); int j=0; while(ans[j]>=1000) { ans[j+1] += ans[j]/1000; ans[j++] %= 1000; } len=max(len,j); } printf("Case #%d: %lld",o,ans[len]); for(int i=len-1;i>=0;i--) { if(ans[i]>=100) printf("%lld",ans[i]); else if(ans[i]>=10) printf("0%lld",ans[i]); else printf("00%lld",ans[i]); } printf("\n");
完整代码

#include <bits/stdc++.h> #define P pair<ll,ll> #define mp(i,j) make_pair(i,j) #define F first #define S second #define MAXN 100005 #define ll long long using namespace std; vector <P> vec[MAXN]; ll dis[MAXN], son[MAXN], dp[MAXN]; ll n, m, ans[MAXN]; void dfs1(ll u,ll f) { son[u]=1; for(int i=0;i<vec[u].size();i++) { ll v=vec[u][i].F, w=vec[u][i].S; if(v==f) continue; dfs1(v,u); son[u]+=son[v]; dis[u]+=dis[v]+son[v]*w; } } void dfs2(int u,int f) { for(int i=0;i<vec[u].size();i++) { ll v=vec[u][i].F, w=vec[u][i].S; if(v==f) continue; dp[v]=dp[u]+(n-2*son[v])*w; dfs2(v,u); } } int main() { int t; scanf("%d",&t); for(int o=1;o<=t;o++) { for(int i=1;i<=n;i++) vec[i].clear(); memset(dis,0,sizeof(dis)); memset(son,0,sizeof(son)); memset(dp,0,sizeof(dp)); scanf("%lld",&n); for(int i=1;i<n;i++) { ll u,v,w; scanf("%lld%lld%lld",&u,&v,&w); vec[u].push_back(mp(v,w)); vec[v].push_back(mp(u,w)); } dfs1(1,0); dp[1]=dis[1]; dfs2(1,0); sort(dp+1,dp+1+n); int len=0; memset(ans,0,sizeof(ans)); for(ll i=1;i<n;i++) { ans[0] += dp[i]*(n-i); int j=0; while(ans[j]>=1000) { ans[j+1] += ans[j]/1000; ans[j++] %= 1000; } len=max(len,j); } printf("Case #%d: %lld",o,ans[len]); for(int i=len-1;i>=0;i--) { if(ans[i]>=100) printf("%lld",ans[i]); else if(ans[i]>=10) printf("0%lld",ans[i]); else printf("00%lld",ans[i]); } printf("\n"); } return 0; }

#include <bits/stdc++.h> #define P pair<int,int> #define mp(i,j) make_pair(i,j) #define F first #define S second #define MAXN 100005 using namespace std; vector <P> vec[MAXN]; int son[MAXN]; int n, m; __int128 dis[MAXN], dp[MAXN]; void dfs1(int u,int f) { son[u]=1; for(int i=0;i<vec[u].size();i++) { int v=vec[u][i].F, w=vec[u][i].S; if(v==f) continue; dfs1(v,u); son[u]+=son[v]; dis[u]+=dis[v]+son[v]*w; } } void dfs2(int u,int f) { for(int i=0;i<vec[u].size();i++) { int v=vec[u][i].F, w=vec[u][i].S; if(v==f) continue; dp[v]=dp[u]+(n-2*son[v])*w; dfs2(v,u); } } void print(__int128 ans) { if(ans>9) print(ans/10); printf("%c",‘0‘+ans%10); } int main() { int t; scanf("%d",&t); for(int o=1;o<=t;o++) { for(int i=1;i<=n;i++) vec[i].clear(); memset(dis,0,sizeof(dis)); memset(son,0,sizeof(son)); memset(dp,0,sizeof(dp)); scanf("%d",&n); for(int i=1;i<n;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); vec[u].push_back(mp(v,w)); vec[v].push_back(mp(u,w)); } dfs1(1,0); dp[1]=dis[1]; dfs2(1,0); sort(dp+1,dp+1+n); __int128 ans=0; for(int i=1;i<n;i++) ans += dp[i]*(n-i); printf("Case #%d: ",o); print(ans);printf("\n"); } return 0; }
原文:https://www.cnblogs.com/zquzjx/p/9441993.html