一、信息熵
- 衡量信息的不确定度;

1)理论提出
- 信息论之父 C. E. Shannon 指出:任何信息都存在冗余,冗余大小与信息中每个符号(数字、字母或单词)的出现概率或者说不确定性有关。
- Shannon 把信息中排除了冗余后的平均信息量称为“信息熵”。
- 通常,一个信源发送出什么符号是不确定的(不同的符号可以看做不同的样本类型),衡量它可以根据其出现的概率来度量。概率大,出现机会多,不确定性小;反之就大。
2)基本内容
- 根据事件发生的概率 P,可得出发生该事件的不确定性:
 ;
;
- 不同事件的不确定性可以相加:f(P1, P2) = f(P1) + f(P2);
- 一个数据集的不确定性:f(P1, P2, ... , Pk) = f(P1) + ... + f(Pk) = H
- 在信源中,考虑的不是某一单个符号发生的不确定性,而是要考虑这个信源所有可能发生情况的平均不确定性。若信源符号有n种取值:U1…Ui…Un,对应概率为:P1…Pi…Pn,且各种符号的出现彼此独立。这时,信源的平均不确定性应当为单个符号不确定性-logPi的统计平均值(E),可称为信息熵,即
 ,式中对数一般取2为底,单位为比特。但是,也可以取其它对数底,采用其它相应的单位,它们间可用换底公式换算。
,式中对数一般取2为底,单位为比特。但是,也可以取其它对数底,采用其它相应的单位,它们间可用换底公式换算。
二、基尼系数
- 百科:基尼系数
- 多用于经济学中,分析国家贫富差距;
- 基尼系数是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。基尼系数介于0-1之间,基尼系数越大,表示不平等程度越高;
- 有赫希曼提出,而不是基尼;
1)通用算法
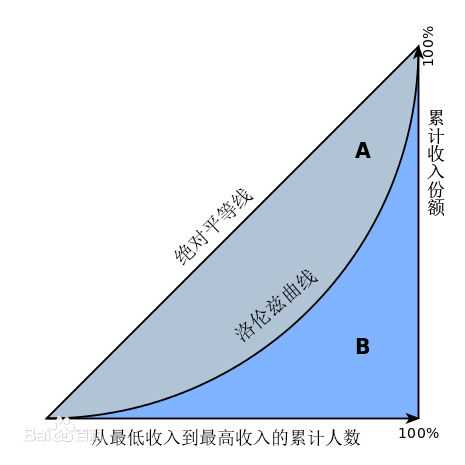
- 赫希曼根据洛伦茨曲线提出的判断分配平等程度的指标。设实际收入分配曲线和收入分配绝对平等曲线之间的面积为A,实际收入分配曲线右下方的面积为B。并以A除以(A+B)的商表示不平等程度;
- 如果A为零,基尼系数为零,表示收入分配完全平等;
- 如果B为零则系数为1,收入分配绝对不平等。
- 收入分配越是趋向平等,洛伦茨曲线的弧度越小,基尼系数也越小,反之,收入分配越是趋向不平等,洛伦茨曲线的弧度越大,那么基尼系数也越大。
统计学基础(二):信息熵、基尼系数
原文:https://www.cnblogs.com/volcao/p/9478193.html