定义:B-树是一类树,包括B-树、B+树、B*树等,是一棵自平衡的搜索树,它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。B-树是专门为外部存储器设计的,如磁盘,它对于读取和写入大块数据有良好的性能,所以一般被用在文件系统及数据库中。
先来看看为什么会出现B-树这类数据结构。
传统用来搜索的平衡二叉树有很多,如 AVL 树,红黑树等。这些树在一般情况下查询性能非常好,但当数据非常大的时候它们就无能为力了。原因当数据量非常大时,内存不够用,大部分数据只能存放在磁盘上,只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns,而磁盘在 10 ms 左右。速度相差了近 5 个数量级,磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能?减少磁盘 IO 次数,像 AVL 树,红黑树这类平衡二叉树从设计上无法“迎合”磁盘。
关于磁盘可参考 浅谈计算机中的存储模型(四)磁盘
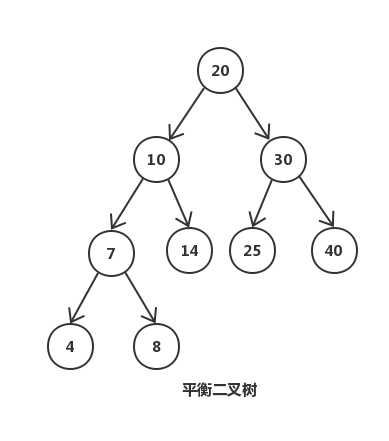
上图是一颗简单的平衡二叉树,平衡二叉树是通过旋转来保持平衡的,而旋转是对整棵树的操作,若部分加载到内存中则无法完成旋转操作。其次平衡二叉树的高度相对较大为 log n(底数为2),这样逻辑上很近的节点实际可能非常远,无法很好的利用磁盘预读(局部性原理),所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。
空间局部性原理:如果一个存储器的某个位置被访问,那么将它附近的位置也会被访问。
我们从“迎合”磁盘的角度来看看B-树的设计。
索引的效率依赖与磁盘 IO 的次数,快速索引需要有效的减少磁盘 IO 次数,如何快速索引呢?索引的原理其实是不断的缩小查找范围,就如我们平时用字典查单词一样,先找首字母缩小范围,再第二个字母等等。平衡二叉树是每次将范围分割为两个区间。为了更快,B-树每次将范围分割为多个区间,区间越多,定位数据越快越精确。那么如果节点为区间范围,每个节点就较大了。所以新建节点时,直接申请页大小的空间(磁盘是按 block 分的,一般为 512 Byte。磁盘 IO 一次读取若干个 block,我们称为一页,具体大小和操作系统有关,一般为 4 k,8 k或 16 k),计算机内存分配是按页对齐的,这样就实现了一个节点只需要一次 IO。

上图是一棵简化的B-树,多叉的好处非常明显,有效的降低了B-树的高度,为底数很大的 log n,底数大小与节点的子节点数目有关,一般一棵B-树的高度在 3 层左右。层数低,每个节点区确定的范围更精确,范围缩小的速度越快。上面说了一个节点需要进行一次 IO,那么总 IO 的次数就缩减为了 log n 次。B-树的每个节点是 n 个有序的序列(a1,a2,a3…an),并将该节点的子节点分割成 n+1 个区间来进行索引(X1< a1, a2 < X2 < a3, … , an+1 < Xn < anXn+1 > an)。
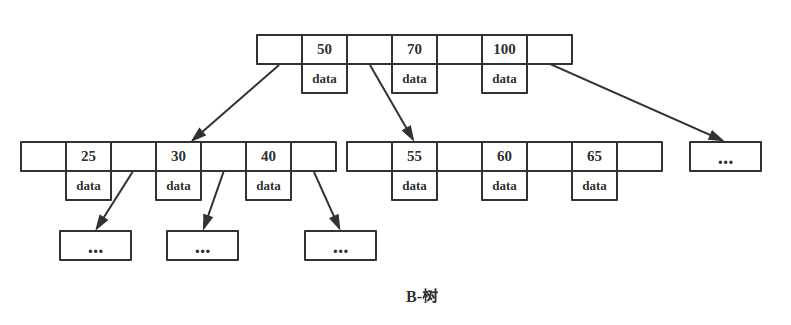
上图是一颗B-树,B-树的每个节点有 d~2d 个 key,这个因子指明了树的分裂及合并的规则,这个规则维持了B-树的平衡。
B-树的插入和删除就不具体介绍了,很多资料都描述了这一过程。在普通平衡二叉树中,插入删除后若不满足平衡条件则进行 旋转 操作,而在B-树中,插入删除后不满足条件则进行分裂及合并操作。
简单叙述下分裂及合并操作。
分裂:如果有一个节点有 2d 个 key,增加一个后为 2d+1 个 key,不符合上述规则 B-树的每个节点有 d~2d 个 key,大于 2d,则将该节点进行分裂,分裂为两个 d 个 key 的节点并将中值 key 归还给父节点。
合并:如果有一个节点有 d 个 key,删除一个后为 d-1 个 key,不符合上述规则 B-树的每个节点有 d~2d 个 key,小于 d,则将该节点进行合并,合并后若满足条件则合并完成,不满足则均分为两个节点。
B-树的查找
我们来看看B-树的查找,假设每个节点有 n 个 key值,被分割为 n+1 个区间,注意,每个 key 值紧跟着 data 域,这说明B-树的 key 和 data 是聚合在一起的。一般而言,根节点都在内存中,B-树以每个节点为一次磁盘 IO,比如上图中,若搜索 key 为 25 节点的 data,首先在根节点进行二分查找(因为 keys 有序,二分最快),判断 key 25 小于 key 50,所以定位到最左侧的节点,此时进行一次磁盘 IO,将该节点从磁盘读入内存,接着继续进行上述过程,直到找到该 key 为止。
查找伪代码
Data* BTreeSearch(Root *node, Key key) { Data* data; if(root == NULL) return NULL; data = BinarySearch(node); if(data->key == key) { return data; }else{ node = ReadDisk(data->next); BTreeSearch(node, key); } }
B+树是B-树的变种,它与B-树的不同之处在于:
如下图为一颗B+树:
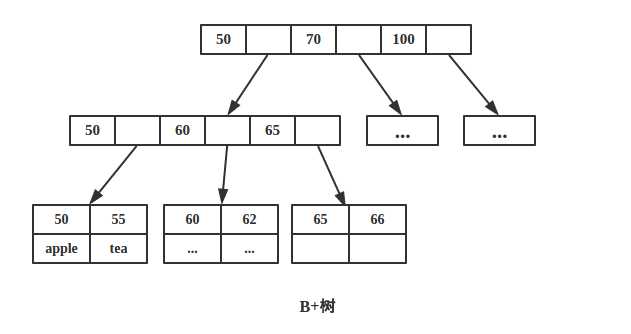
因为内节点并不存储 data,所以一般B+树的叶节点和内节点大小不同,而B-树的每个节点大小一般是相同的,为一页。
为了增加 区间访问性,一般会对B+树做一些优化。
如下图带顺序访问的B+树。
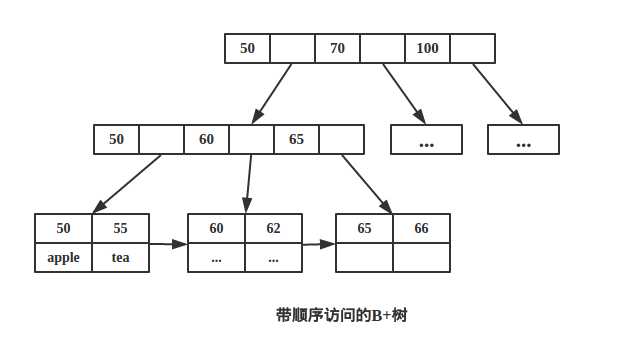
1.B+树内节点不存储数据,所有 data 存储在叶节点导致查询时间复杂度固定为 log n。而B-树查询时间复杂度不固定,与 key 在树中的位置有关,最好为O(1)。
如下所示B-树/B+树查询节点 key 为 50 的 data。
B-树
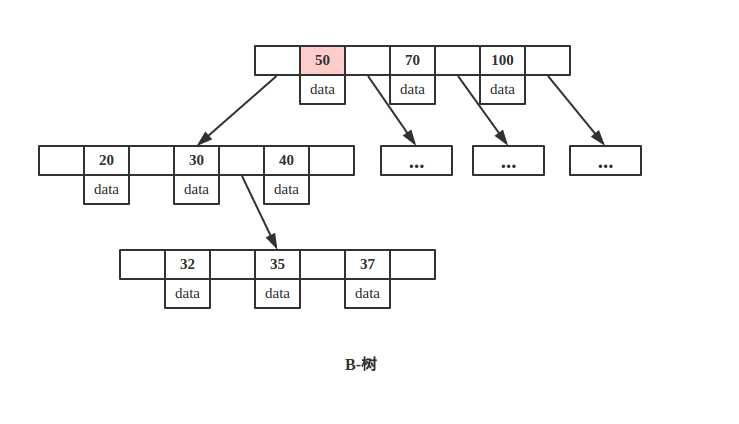
从上图可以看出,key 为 50 的节点就在第一层,B-树只需要一次磁盘 IO 即可完成查找。所以说B-树的查询最好时间复杂度是 O(1)。
B+树
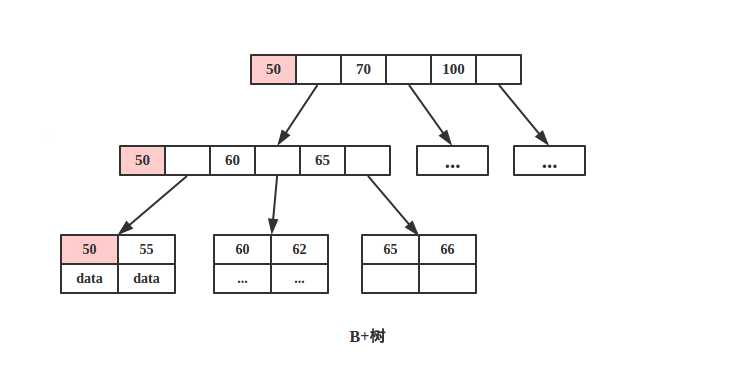
由于B+树所有的 data 域都在根节点,所以查询 key 为 50的节点必须从根节点索引到叶节点,时间复杂度固定为 O(log n)。
2.B+树叶节点两两相连可大大增加区间访问性,可使用在范围查询等,而B-树每个节点 key 和 data 在一起,则无法区间查找。
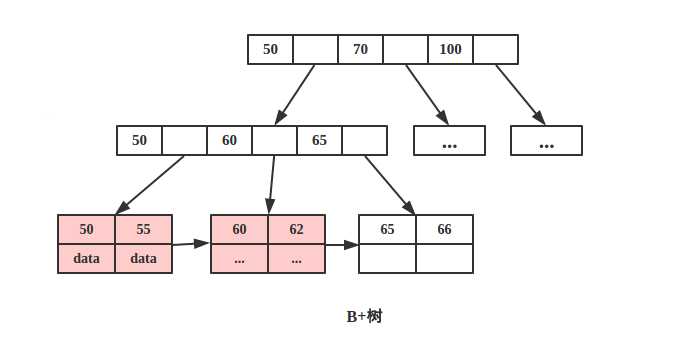
根据空间局部性原理:如果一个存储器的某个位置被访问,那么将它附近的位置也会被访问。
B+树可以很好的利用局部性原理,若我们访问节点 key为 50,则 key 为 55、60、62 的节点将来也可能被访问,我们可以利用磁盘预读原理提前将这些数据读入内存,减少了磁盘 IO 的次数。
当然B+树也能够很好的完成范围查询。比如查询 key 值在 50-70 之间的节点。
3.B+树更适合外部存储。由于内节点无 data 域,每个节点能索引的范围更大更精确
这个很好理解,由于B-树节点内部每个 key 都带着 data 域,而B+树节点只存储 key 的副本,真实的 key 和 data 域都在叶子节点存储。前面说过磁盘是分 block 的,一次磁盘 IO 会读取若干个 block,具体和操作系统有关,那么由于磁盘 IO 数据大小是固定的,在一次 IO 中,单个元素越小,量就越大。这就意味着B+树单次磁盘 IO 的信息量大于B-树,从这点来看B+树相对B-树磁盘 IO 次数少。
这些内容了解后,我们来看为什么 MongoDB 索引选择B-树,而 Mysql (InooDB 引擎)索引选择B+树。
Mysql 大家应该比较熟悉,传统的关系型数据库,下面介绍下 MongoDB。
来看下 wiki 百科上 MongoDB 的定义:
MongoDB (from humongous) is a cross-platform document-oriented database. Classified as a NoSQL database, MongoDB eschews the traditional table-based relational database structure in favor of JSON-like documents with dynamic schemas (MongoDB calls the format BSON)
这段话的大致意思是 MongoDB 是文档型的数据库,是一种 nosql,它使用类 Json 格式保存数据。
文档型数据库和我们常见的关系型数据库不同,一般使用 XML 或 Json 格式来保存数据,归属于聚合型数据库。
键值数据库也属于聚合型数据库,熟悉 Redis 的同学应该很好理解。
举个例子:
加入我们要建立一个电子商务网站,类似淘宝这种将商品销售给用户,那么必须存储用户信息、商品目录、订单、收货地址、账单地址、付款方式等。
看下传统的关系型数据库是如何存储的:
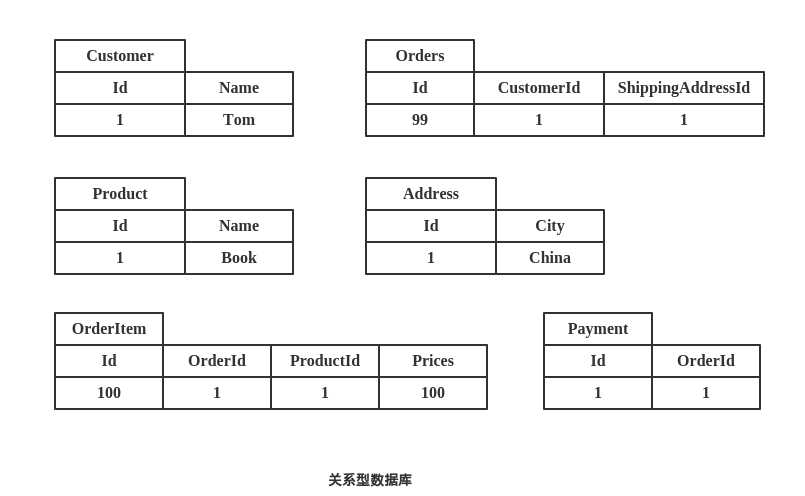
聚合型数据库存储模型:
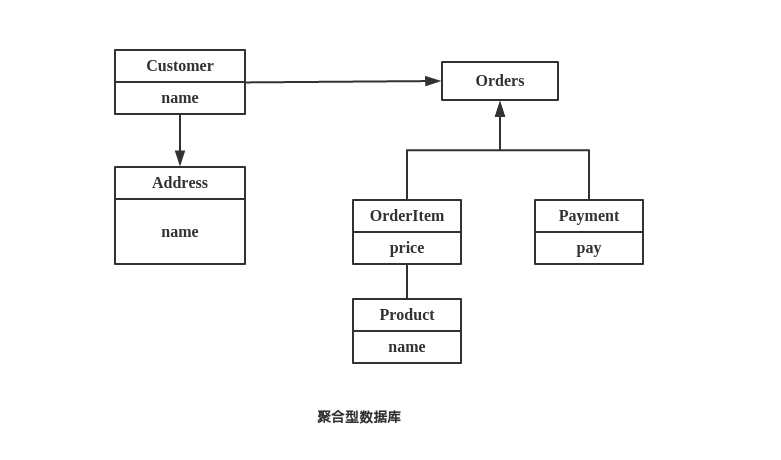
用类似 Json 的格式表示如下:
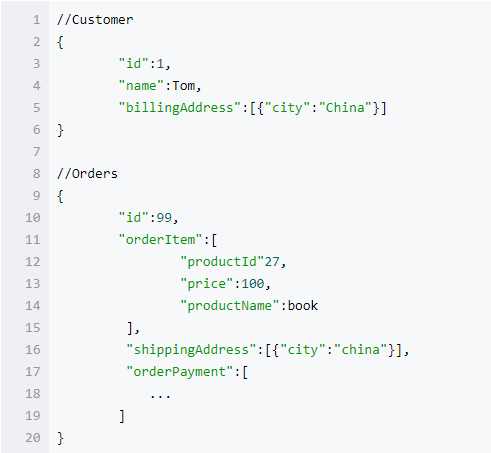
相对于 Mysql 关系型数据库,MongoDB 这类 nosql 适用于数据模型简单,性能要求高的场合。
MongoDB 是一种 nosql,也存储在磁盘上,被设计用在 数据模型简单,性能要求高的场合。性能要求高,看看B/B+树的区别第一点:
B+树内节点不存储数据,所有 data 存储在叶节点导致查询时间复杂度固定为 log n。而B-树查询时间复杂度不固定,与 key 在树中的位置有关,最好为O(1)
我们说过,尽可能少的磁盘 IO 是提高性能的有效手段。MongoDB 是聚合型数据库,而 B-树恰好 key 和 data 域聚合在一起。
Mysql 是一种关系型数据库,区间访问是常见的一种情况,而 B-树并不支持区间访问(可参见上图),而B+树由于数据全部存储在叶子节点,并且通过指针串在一起,这样就很容易的进行区间遍历甚至全部遍历。
见B/B+树的区别第二点:
B+树叶节点两两相连可大大增加区间访问性,可使用在范围查询等,而B-树每个节点 key 和 data 在一起,则无法区间查找。
其次B+树的查询效率更加稳定,数据全部存储在叶子节点,查询时间复杂度固定为 O(log n)。
最后第三点:
B+树更适合外部存储。由于内节点无 data 域,每个节点能索引的范围更大更精确
为什么 MongoDB (索引)使用B-树而 Mysql 使用 B+树
原文:https://www.cnblogs.com/kaleidoscope/p/9481991.html