当我们设计并训练好模型之后,就需要在测试集上进行验证。而当模型在测试集上的效果不佳后,我们就需要从模型在测试集上的误差来源进行分析,进而调整模型。而模型在测试集上的误差主要来自两个方面:偏差(bias)和方差(variance)。
若我们设计的模型为f(x),测试样本为x,yD为样本的标签,y表示样本的真正标签(数据的样本标签并不总是等于真实的样本标签,例如在存在测量等误差),模型在测试样本x上的输出为f(x;D)
使用样本数相同的不同训练集,对f(x)进行训练,会产生多个不同参数的模型。这些模型对测试样本x进行预测,则f(x;D)为随机变量,这些模型的预测期望为

对测试样本产生的方差为

模型输出期望与真正标签的的差别即为偏差

测样样本的标签和真正标签之间的噪声为

假设噪声期望E[y-yD]=0,模型的预测输出和yD的误差为
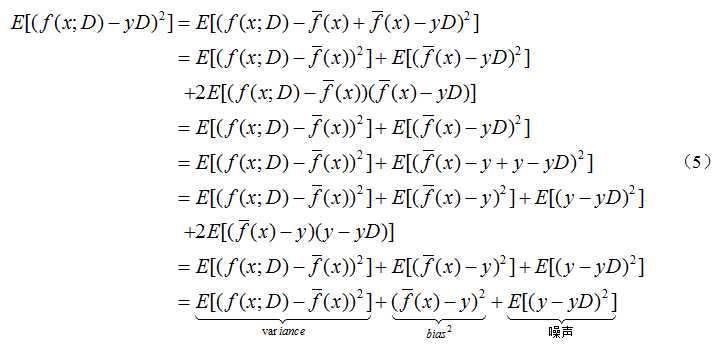
因此有误差可以分解为方差、偏差、噪音;其中噪音是无法进行更正(如在测量身高时会存在一定误差),因此可以从方差和偏差两方面着手。
简单的说,偏差代表了预测期望值跟目标值之间的距离,也就瞄不瞄的准;而方差代表的是预测值跟预测期望的波动情况,也就是在确定瞄准目标后,跟瞄准目标的偏离情况。更形象的如图1-1所示
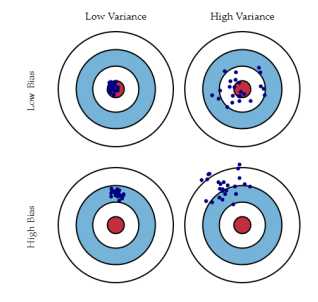
图1-1 方差和偏差
通常我们希望的是低偏差的低方差,也就是我们瞄准目标之后。也能够射中靶心;但是很多时候却不是这样,高偏差和高方差表示的是并没有瞄准目标,而且射出去还偏离了靶心;
已经知道模型的误差由偏差和方差两方面造成的。那么,我们在设计并训练好模型后,应该清楚如何判断我们模型的误差和偏差,并进行模型调整。
如果在设计好模型后,并进行模型训练。在确定训练集数据是“干净”的前提下,如果发现模型一直拟合不了或者拟合之后再训练集上验证结果很糟糕,那么就表示模型的偏差就过大了,也就是我们通常说的欠拟合。
如果在设计并训练好模型之后,模型在训练集上的验证结果很高。但是,在测试集上的结果却很糟糕,那么这就表示模型的方差过大,也就是通常说的欠拟合。
如果模型的方差较大,那我们就需要增加模型的平滑性来减低方差。但增加平滑性,也会使得模型的拟合能力降低,从而导致偏差增大;同样,如果偏差较大,我们想减小偏差,那么就需要增加模型的拟合能力,也同样会增加模型的方差。因此,在偏差和方差之间,我们需要去衡量,取一个最佳值。
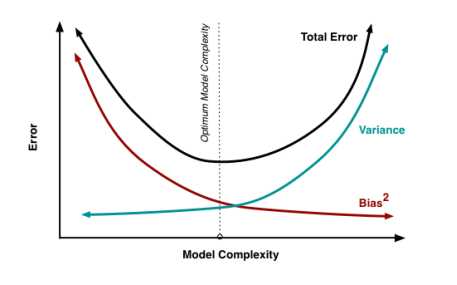
图1-2 偏差和方差的权衡
如图1-3所示,将数据集分为两个部分,其中一部分是训练集,另外一部分是测试集。当我们在训练集上完成多个模型训练,就在测试集上进行验证并根据在测试集上的结果对模型进行调整,最终选择在测试集上最好的模型作为结果。
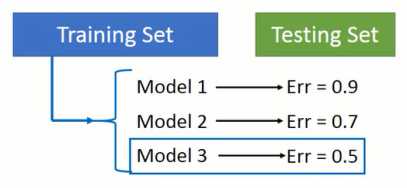
图1-3 不正确的模型选择
上述做法不正确的原因在于,我们发现模型在测试集上的结果并不理想,就会调整模型,使模型在测试集上的表现更好。但是,由于训练集和测试集的数据分布可能会存在“区别”,因此我们在测试集上进行调整的话,其实是把训练集和测试集的“区别”进行调整。但是,当我们将模型放在线上,所接触到的数据的分布跟训练集和测试集都有“区别”,这个时候,模型的整个效果就没有在测试集上表现的那么好。通常还会变差!
为了真正体现模型在验证集上的性能,可以采用如图1-4方法进行模型选择。将训练集分为两部分,一部分是训练集(Training Set),一部分是验证集(Validation Set)。在训练集上训练模型,并在验证集上进行验证。当我们确定那一个模型最好之后,将所有数据集在训练一遍。最后在public Testing Set上进行验证,在public Testing Set上的结果可以反映模型真正的性能。并且不要由于public Testing Set上的效果不佳就去调整模型,因为调整训练集跟public Testing Set之间的区别,并不能真正调整跟线上数据的区别。
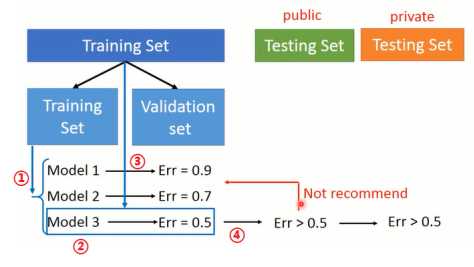
图1-4 交叉验证
在图1-4中,将训练集分为两部分后,对于单个模型只进行一次实验验证,可能会存在误差。因此可以进行多个实验,取平均值可能更好地进行评估,如图1-5所示。
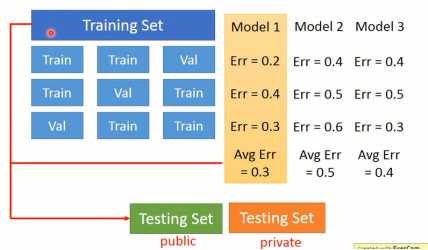
图1-5 N折交叉验证
将所有训练局等分为N分,将其中一份作为验证集,其余为测试集,就可以形成N中训练集和验证集。对于单个模型,分别进行N次试验,取平均值作为最终的验证效果。
手写识别
由于每个人手写角度不一样,可以将图片进行旋转15度
影像辨识
手头上只有从左边开过来的火车,而没有右边开过来的火车;你可以将图像进行翻转
语音辨识
只有男生的“你好”,没有女生的“你好”,可以通过变声器开进行处理
自然语言处理
可以采用翻译软件,将一种语言翻译成为另外一种语言
这是因为,采用投票选择最终预测结果的话,也就是所有模型的输出结果都是相同,因此整个误差中的方差也就被缩小。但是,如果采用投票最终选择的结果是错误的话,那么就会增加了偏差的情况。
越简单的模型通常具有更好的平滑性,因此整个模型的波动就更小,对应的方差也更小;而越复杂的模型,由于能够呈现出更复杂的曲线,整个模型的波动就更大,对应的方差也就更大;因此,模型的平滑性是在减少方差上做出响应。
[2]Understanding the Bias-Variance Trade-off
[3]《机器学习》-周志华
原文:https://www.cnblogs.com/MrPan/p/9484033.html