小T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有 nnn 个矿石,从 111 到 nnn 逐一编号,每个矿石都有自己的重量 wiw_iwi? 以及价值 viv_ivi? 。检验矿产的流程是:
1 、给定 m 个区间 [Li,Ri];
2 、选出一个参数 W ;
3 、对于一个区间 [Li,Ri],计算矿石在这个区间上的检验值 Yi :
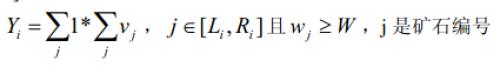
这批矿产的检验结果 Y 为各个区间的检验值之和。即: Y1+Y2...+Ym?
若这批矿产的检验结果与所给标准值 S 相差太多,就需要再去检验另一批矿产。小T不想费时间去检验另一批矿产,所以他想通过调整参数W 的值,让检验结果尽可能的靠近标准值 S ,即使得 S−Y 的绝对值最小。请你帮忙求出这个最小值。
输入格式:
第一行包含三个整数 n,m,S,分别表示矿石的个数、区间的个数和标准值。
接下来的 n 行,每行 2 个整数,中间用空格隔开,第 i+1 行表示 i 号矿石的重量 wi 和价值 vi? 。
接下来的 m 行,表示区间,每行 2 个整数,中间用空格隔开,第 i+n+1 行表示区间 [Li,Ri]的两个端点 Li和 Ri 。注意:不同区间可能重合或相互重叠。
输出格式:
一个整数,表示所求的最小值。
暴力是不行的啦,而我又不会别的qwq
所以我就想办法开始优化
一看w才1e6,好办,可以二分答案了。
每次二分一个答案,然后验证
如果二分出来的答案s-y小于0,那么可能最优解在他的右边
反之亦然
记得每次都要更新答案哟。
怎么验证呢?
我们就要用到前缀和
每次二分出一个数,我就按这个条件O(N)算出前缀和
询问的回答就可以O(1)了
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define rii register int i #define rij register int j #define inf 19260817 #define int long long using namespace std; long long qzhv[1000005],qzhw[1000005],s,n,m,v[200005],w[200005]; long long maxn,minx; long long z[200005],y[200005]; long long find(int wz) { long long ans=0; memset(qzhv,0,sizeof(qzhv)); memset(qzhw,0,sizeof(qzhw)); for(rii=1;i<=n;i++) { qzhv[i]=qzhv[i-1]; qzhw[i]=qzhw[i-1]; if(w[i]>=wz) { qzhw[i]++; qzhv[i]+=v[i]; } } for(rii=1;i<=m;i++) { long long ltt=z[i]; long long kkk=y[i]; ans+=(qzhw[kkk]-qzhw[ltt-1])*(qzhv[kkk]-qzhv[ltt-1]); } return ans; } long long qabs(long long val) { if(val>0) { return val; } else { return val*(-1); } } signed main() { maxn=-inf; minx=inf; scanf("%d%d%lld",&n,&m,&s); for(rii=1;i<=n;i++) { scanf("%d%d",&w[i],&v[i]); maxn=max(maxn,w[i]); minx=min(minx,w[i]); } for(rii=1;i<=m;i++) { scanf("%d%d",&z[i],&y[i]); } int l=minx-1; int r=maxn+2; minx=9999999999999999; while(l!=r) { if(r-l==1) { minx=min(minx,min(qabs(find(l)-s),qabs(find(r)-s))); break; } int mid=(l+r)/2; long long qaq=find(mid); minx=min(minx,qabs(qaq-s)); qaq=qaq-s; if(qaq<0) { r=mid; } else { l=mid; } } cout<<minx; }
原文:https://www.cnblogs.com/ztz11/p/9472859.html