突然发现网上关于点分和动态点分的教程好像很少……蒟蒻开篇blog记录一下吧……有问题的话欢迎大家指出
参考文献:https://www.cnblogs.com/LadyLex/p/8006488.html
https://blog.csdn.net/qq_39553725/article/details/77542223
https://blog.csdn.net/zzkksunboy/article/details/70244945
前言
一般来说,对于大规模处理树上路径,我们会对整棵树进行分治。而树分治有两种,一种是边分治,不在本文考虑范围内(主要是我不会)所以暂且不提,另外一种就是点分治。
淀粉质,啊呸,点分治,顾名思义,就是把树上的节点拆开来进行分治,每一次把树给拆成好几棵子树,然后再继续递归下去,直到算出所有的答案
分治点
既然是分治,我们肯定每一次都要选择一个点,从他开始分治下去。那么考虑我们如何选择这个点呢?我们发现,每一次处理完一个点之后,我们都要递归进它的子树,那么时间复杂度受到它最大的子树的大小的影响。比如,如果原树是一条链,我们选择链首,一路递归下去,时间复杂度毫无疑问是$O(n^2)$的(那还不如别学了直接打暴力)。所以,我们要让每一次选到的点的最大子树最小。
实际上,一棵树的最大子树最小的点有一个名称,叫做重心。
时间复杂度
考虑一下为什么每一次都选择重心,时间复杂度就是对的呢?
因为重心有一个很重要的性质,每一个子树的大小都不超过$n/2$
考虑为什么呢?我们可以用反证法来证明(这里感谢zzk大佬的证明)
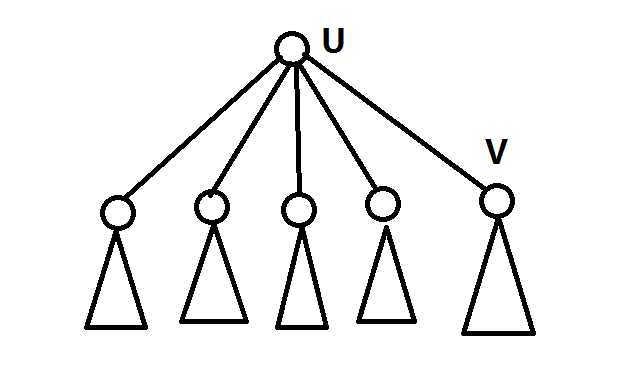
考虑有如上这么一棵树,其中点$u$是重心,$son[u]$表示$u$点的最大的子树的大小,$v$是点$u$的最大子树,且$size[v]>size[u]/2$
因为$size[v]>size[u]/2$,其他子树加上点$u$的节点数小于$size[u]/2$,那么不难发现,我们选择点$v$作为重心,$son[v]=size[v]-1<son[u]$,那么很明显$u$不满足重心的定义
于是每一次找到重心,递归的子树大小是不超过原树大小的一半的,那么递归层数不会超过$O(logn)$层,时间复杂度为$O(nlogn)$
求重心
然而重心如何求呢?直接暴力,我们$dfs$整棵树,可以$O(n)$的求出树的重心
还是贴代码好了
void getrt(int u,int fa){ //sz表示子树的大小,son表示点的最大子树的大小 //cmax(a,b)表示如果b>a则a=b //个人习惯这样写,或者直接写成a=max(a,b) sz[u]=1,son[u]=0; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]||v==fa) continue; getrt(v,u); sz[u]+=sz[v]; cmax(son[u],sz[v]); } //size表示整棵树的大小 //因为这是一棵无根树,所以包括它的父亲在内的那一坨也应该算作它的子树 cmax(son[u],size-sz[u]); if(son[u]<mx) mx=son[u],rt=u; }
于是就可以愉快的$O(n)$求出重心(~ ̄▽ ̄)~
实现
还是先贴代码好了
void divide(int u){ ans+=solve(u,0);//把当前节点的答案加上去 vis[u]=1;//把节点标记,防止陷入死循环 for(int i=head[u];i;i=Next[i]){ //分别处理每一棵子树 int v=ver[i]; if(vis[v]) continue; ans-=solve(v,edge[i]);//容斥原理,下面说 mx=inf,rt=0,size=sz[v]; //把所有信息更新,递归进子树找重心,并继续分治 getrt(v,0); divide(rt); } }
上面其他的应该都好理解,除了这一句 ans-=solve(v,edge[i]);
考虑一下这棵树
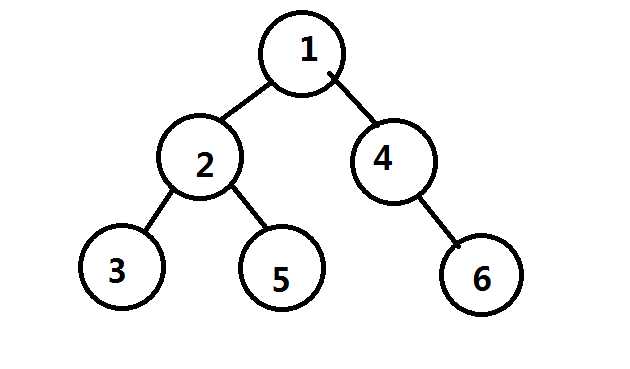
考虑一下,从点$1$出发的路径有以下几条
$1->4$
$1->4->6$
$1->2$
$1->2->3$
$1->2->5$
然后我们为了求贡献,会将路径两两合并
然而合并$1->2->3$和$1->2->5$这两条路径实际上是不合法的,因为出现了重边
所以要减去$2$这一棵子树中的所有路径两两合并的贡献
然后回头来看代码 ans+=solve(u,0); ans-=solve(v,edge[i]);
看到没?第二个参数不一样,这样在考虑子树中两两合并时的贡献时就不会把这一条边的贡献给漏掉了
然后只要递归继续找就可以(*^▽^*)
注意点
我上面点分时的代码有一个问题,就是这一句 size=sz[v];
上面那个代码是我当初刚学点分的时候码的,然后后来看了一些文章,觉着这里有问题
这里$size$表示的是进去找重心时整棵子树的大小,一般的文章里都是写成上面这样的
然而看了LadyLex大佬的代码,却发现这种写法实际上有问题
因为,如果当初$dfs$找重心的时候,点$v$是点$u$的父亲怎么办呢?那么$sz[v]$实际上是包含$sz[u]$的,也就是说,$sz[v]$是这一整棵树的大小,而不是要递归进去的子树的大小!!不是要递归进去的子树的大小!!不是要递归进去的子树的大小!!(因为很重要所以说三遍)
实际上,我做点分到现在,看了那么多文章,抄了那么多题解,似乎只有LadyLex大佬一个人是考虑到这一点的
然而很尴尬的是似乎从来没有TLE过……
当然也有可能不用考虑这一点时间复杂度也是正确的,如果真的这样的话米娜桑麻烦下面跟我说一声我sb了
所以实际上上面的点分应该这样写
void divide(int u){ ans+=solve(u,0); vis[u]=1; int totsz=size;//记录一下整棵树的大小 for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]) continue; ans-=solve(v,edge[i]); mx=inf,rt=0; size=sz[v]>sz[u]?totsz-sz[u]:sz[v]; //如果v的sz大于u,说明dfs的时候v是u的父亲 //那么实际上v这一棵子树的大小是原树的大小减去u的子树的大小 //实际上就相当于上面找重心时的容斥 getrt(v,0); divide(rt); } }
ps:因为我也分不清自己什么时候做的题,什么时候发现这一点的了……所以下面的例题里可能有的代码不是按这种写法……米娜桑自己注意一下……
例题
讲了这么多……然而实际上似乎并没有什么用……还是来讲几道题好了……

//minamoto #include<bits/stdc++.h> #define N 40005 #define M 80005 #define ll long long #define inf 0x3f3f3f3f using namespace std; #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<15,stdin),p1==p2)?EOF:*p1++) char buf[1<<15],*p1=buf,*p2=buf; template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} inline int read(){ #define num ch-‘0‘ char ch;bool flag=0;int res; while(!isdigit(ch=getc())) (ch==‘-‘)&&(flag=true); for(res=num;isdigit(ch=getc());res=res*10+num); (flag)&&(res=-res); #undef num return res; } int ver[M],Next[M],head[N],edge[M]; int n,tot,root;ll k; void add(int u,int v,int e){ ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e; } int sz[N],vis[N],mx,size; ll d[N],q[N],l,r; void getroot(int u,int fa){ sz[u]=1;int num=0; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(v==fa||vis[v]) continue; getroot(v,u); sz[u]+=sz[v]; cmax(num,sz[v]); } cmax(num,size-sz[u]); if(num<mx) mx=num,root=u; } void getdis(int u,int fa){ q[++r]=d[u]; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(v==fa||vis[v]) continue; d[v]=d[u]+edge[i]; getdis(v,u); } } ll calc(int u,int val){ r=0; d[u]=val; getdis(u,0); ll sum=0;l=1; sort(q+1,q+r+1); while(l<r){ if(q[l]+q[r]<=k) sum+=r-l,++l; else --r; } return sum; } ll ans=0; void dfs(int u){ ans+=calc(u,0); vis[u]=1; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]) continue; ans-=calc(v,edge[i]); size=sz[v]; mx=inf; getroot(v,0); dfs(root); } } int main(){ //freopen("testdata.in","r",stdin); n=read(); for(int i=1;i<n;++i){ int u=read(),v=read(),e=read(); add(u,v,e); } k=read(); size=n; mx=inf; getroot(1,0); dfs(root); printf("%lld",ans); return 0; }
poj1741tree
给一颗n个节点的树,每条边上有一个距离v。定义d(u,v)为u到v的最小距离。给定k值,求有多少点对(u,v)使u到v的距离小于等于k。
点分的板子……好像基本都是板子套进去……就是注意合并的时候二分保证复杂度
bzoj2152 聪聪可可
聪聪和可可是兄弟俩,他们俩经常为了一些琐事打起来,例如家中只剩下最后一根冰棍而两人都想吃、两个人都想玩儿电脑(可是他们家只有一台电脑)……遇到这种问题,一般情况下石头剪刀布就好了,可是他们已经玩儿腻了这种低智商的游戏。
他们的爸爸快被他们的争吵烦死了,所以他发明了一个新游戏:由爸爸在纸上画n个“点”,并用n-1条“边”把这n个“点”恰好连通(其实这就是一棵树)。并且每条“边”上都有一个数。接下来由聪聪和可可分别随即选一个点(当然他们选点时是看不到这棵树的),如果两个点之间所有边上数的和加起来恰好是3的倍数,则判聪聪赢,否则可可赢。
聪聪非常爱思考问题,在每次游戏后都会仔细研究这棵树,希望知道对于这张图自己的获胜概率是多少。现请你帮忙求出这个值以验证聪聪的答案是否正确。
输入格式:
输入的第1行包含1个正整数n。后面n-1行,每行3个整数x、y、w,表示x号点和y号点之间有一条边,上面的数是w。
输出格式:
以即约分数形式输出这个概率(即“a/b”的形式,其中a和b必须互质。如果概率为1,输出“1/1”)。
【样例说明】
13组点对分别是(1,1) (2,2) (2,3) (2,5) (3,2) (3,3) (3,4) (3,5) (4,3) (4,4) (5,2) (5,3) (5,5)。
【数据规模】
对于100%的数据,n<=20000。
很明显,思路就是统计长度为$3$的倍数的路径的条数,然后除以路径总和就是答案
先贴一句话题解:先用点分计算出路径长度,把路径长度对$3$取模,然后用$sum[1],sum[2],sum[0]$表示模数是$1,2,3$的情况的总数,那么就是$ans+=sum[1]*sum[2]*2+sum[0]*sum[0]$,最后答案就是$ans/(n*n)$
用人话说的话,我们可以先考虑一个点,用$sum[1,2,3]$分别表示从以这一个点为根,往下的长度对$3$取模余数是$1,2,3$的路径条数,那么所有经过这一个点的路径有多少条呢?所有长度为$1$和$2$的路径可以两两拼起来成为一条,反着也可以,长度为$3$的路径可以两两拼。所以答案就加上上面那个式子
然后进行点分,不断递归就可以了

1 //minamoto 2 #include<iostream> 3 #include<cstdio> 4 #define ll long long 5 #define inf 0x3f3f3f3f 6 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) 7 char buf[1<<21],*p1=buf,*p2=buf; 8 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} 9 inline int read(){ 10 #define num ch-‘0‘ 11 char ch;bool flag=0;int res; 12 while(!isdigit(ch=getc())) 13 (ch==‘-‘)&&(flag=true); 14 for(res=num;isdigit(ch=getc());res=res*10+num); 15 (flag)&&(res=-res); 16 #undef num 17 return res; 18 } 19 char sr[1<<21],z[20];int C=-1,Z; 20 inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;} 21 inline void print(int x){ 22 if(C>1<<20)Ot();if(x<0)sr[++C]=45,x=-x; 23 while(z[++Z]=x%10+48,x/=10); 24 while(sr[++C]=z[Z],--Z); 25 } 26 const int N=20005,mod=3; 27 int head[N],Next[N<<1],edge[N<<1],ver[N<<1];ll ans=0; 28 int sz[N],son[N],sum[4],vis[N]; 29 int size,mx,rt,n,tot; 30 inline void add(int u,int v,int e){ 31 ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; 32 ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e; 33 } 34 void getrt(int u,int fa){ 35 sz[u]=1,son[u]=0; 36 for(int i=head[u];i;i=Next[i]){ 37 int v=ver[i]; 38 if(vis[v]||v==fa) continue; 39 getrt(v,u); 40 sz[u]+=sz[v]; 41 cmax(son[u],sz[v]); 42 } 43 cmax(son[u],size-sz[u]); 44 if(son[u]<mx) mx=son[u],rt=u; 45 } 46 void query(int u,int fa,int d){ 47 ++sum[d%mod]; 48 for(int i=head[u];i;i=Next[i]){ 49 int v=ver[i]; 50 if(vis[v]||v==fa) continue; 51 query(v,u,(d+edge[i])%mod); 52 } 53 } 54 ll solve(int rt,int d){ 55 sum[0]=sum[1]=sum[2]=0; 56 query(rt,0,d); 57 ll res=1ll*sum[1]*sum[2]*2+1ll*sum[0]*sum[0]; 58 return res; 59 } 60 void divide(int u){ 61 ans+=solve(u,0); 62 vis[u]=1; 63 for(int i=head[u];i;i=Next[i]){ 64 int v=ver[i]; 65 if(vis[v]) continue; 66 ans-=solve(v,edge[i]); 67 mx=inf,rt=0,size=sz[v]; 68 getrt(v,0); 69 divide(rt); 70 } 71 } 72 inline ll gcd(ll a,ll b){ 73 while(b^=a^=b^=a%=b); 74 return a; 75 } 76 int main(){ 77 n=read(); 78 for(int i=1;i<n;++i){ 79 int u=read(),v=read(),e=read(); 80 add(u,v,e%3); 81 } 82 mx=inf,size=n,ans=0,rt=0; 83 getrt(1,0),divide(rt); 84 ll p=n*n,GCD=gcd(ans,p); 85 print(ans/GCD),sr[++C]=‘/‘,print(p/GCD); 86 Ot(); 87 return 0; 88 }
给定一棵有n个点的树
询问树上距离为k的点对是否存在。
输入格式:
n,m 接下来n-1条边a,b,c描述a到b有一条长度为c的路径
接下来m行每行询问一个K
输出格式:
对于每个K每行输出一个答案,存在输出“AYE”,否则输出”NAY”(不包含引号)
对于30%的数据n<=100
对于60%的数据n<=1000,m<=50
对于100%的数据n<=10000,m<=100,c<=1000,K<=10000000
考虑一下$k$的范围,干脆预处理出答案然后直接$O(1)$回答询问吧……
就是把每一个节点向下长度为$d$的路径有多少条记下来,然后两两合并,时间复杂度$O(n^2)$,不知道为毛能过……

//minamoto #include<cstdio> #include<iostream> #define inf 0x3f3f3f3f #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) char buf[1<<21],*p1=buf,*p2=buf; template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;} inline int read(){ #define num ch-‘0‘ char ch;bool flag=0;int res; while(!isdigit(ch=getc())) (ch==‘-‘)&&(flag=true); for(res=num;isdigit(ch=getc());res=res*10+num); (flag)&&(res=-res); #undef num return res; } const int N=10005; int ans[10000005]; int ver[N<<1],head[N],Next[N<<1],edge[N<<1]; int sz[N],son[N],st[N];bool vis[N]; int n,m,size,mx,rt,tot,top; inline void add(int u,int v,int e){ ver[++tot]=v,Next[tot]=head[u],head[u]=tot,edge[tot]=e; ver[++tot]=u,Next[tot]=head[v],head[v]=tot,edge[tot]=e; } void getrt(int u,int fa){ sz[u]=1,son[u]=0; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]||v==fa) continue; getrt(v,u); sz[u]+=sz[v],cmax(son[u],sz[v]); } cmax(son[u],size-sz[u]); if(son[u]<mx) mx=son[u],rt=u; } void query(int u,int fa,int d){ st[++top]=d; for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]||v==fa) continue; query(v,u,d+edge[i]); } } void solve(int rt,int d,int f){ top=0; query(rt,0,d); if(f){ for(int i=1;i<top;++i) for(int j=i+1;j<=top;++j) ++ans[st[i]+st[j]]; } else{ for(int i=1;i<top;++i) for(int j=i+1;j<=top;++j) --ans[st[i]+st[j]]; } } void divide(int u){ vis[u]=true; solve(u,0,1); for(int i=head[u];i;i=Next[i]){ int v=ver[i]; if(vis[v]) continue; solve(v,edge[i],0); mx=inf,rt=0,size=sz[v]; getrt(v,0); divide(rt); } } int main(){ n=read(),m=read(); for(int i=1;i<n;++i){ int u=read(),v=read(),e=read(); add(u,v,e); } rt=0,mx=inf,size=n; getrt(1,0),divide(rt); while(m--){ int k=read(); puts(ans[k]?"AYE":"NAY"); } return 0; }
然后就是关于点分的一些题单了,基本我都写(chao)了题解的
然后动态点分还是明天再讲好了
施工现场
原文:https://www.cnblogs.com/bztMinamoto/p/9489473.html