嗯哼,今天记录下采用Java编写的爬山算法(Hill Algorithm)求解TSP问题。
爬山算法与其他智能算法类似,是一种用来求解多峰函数最值的算法,爬山算法的基本思想是新解不劣于当前解则转移,否则不转移。通俗的解说是兔子爬山的例子,其他博客上介绍的十分细致,在此不再赘述。
爬山算法的算法描述为:
下面上干货:
1 package Hill_Algorithm; 2 3 import java.util.Random; 4 5 /** 6 * @file_name SATSP.java 7 * @author xzl 8 * @date 2018年8月11日 9 * @detail Simulated Annealing to solve Travel Salesman Problem 10 */ 11 12 public class HATSP { 13 14 public static double[] HA() { 15 16 //参数列表 17 int MaxCount = 10000; 18 19 //初始化 20 double[][] xy = Data.XY(); 21 int N = xy.length; 22 23 double bs ; 24 double Nowbs; 25 int[] BS = new int[N]; 26 int[] S = new int[N]; 27 28 //生成随机初始解 29 for (int i = 0; i < N; i++) { 30 S[i] = i + 1; 31 } 32 for (int k = 0; k < N;k++) { 33 Random rand = new Random(); 34 int r = rand.nextInt(N); 35 int tmp; 36 tmp = S[r]; 37 S[r] = S[k]; 38 S[k] = tmp; 39 } 40 bs = Evaluate.Eval(S); 41 42 //进入迭代过程 43 int effI = 0; 44 for (int count = 0; count < MaxCount; count++) { 45 46 //产生一个新解 47 int[] newS = new int[N]; 48 double R = Math.random(); 49 50 if (R < 0.33) { 51 newS = Sharking.Swap(S); 52 }else if (R > 0.67) { 53 newS = Sharking.Insert(S); 54 }else { 55 newS = Sharking.Flip(S); 56 } 57 Nowbs = Evaluate.Eval(newS); 58 59 //解的更新 60 if (Nowbs < bs) { 61 bs = Nowbs; 62 effI++; 63 System.out.println( "第 " + effI + "次有效迭代出现在第 " + count + "次迭代,对应的解为 " + bs); 64 System.arraycopy(newS, 0, BS, 0, N); 65 } 66 System.arraycopy(BS, 0, S, 0, N); 67 } 68 69 //结果输出 70 double[] Solution = new double[N + 2]; 71 Solution[0] = bs; 72 Solution[1] = MaxCount; 73 74 for (int i = 2; i < N+2; i++) { 75 Solution[i] = BS[i-2]; 76 } 77 return Solution; 78 } 79 }
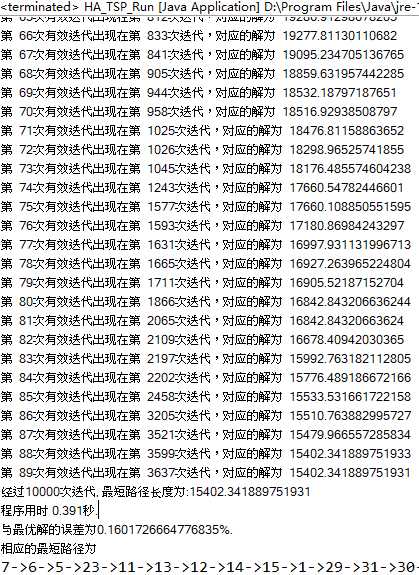
求解31个城市的TSP,求解结果如下,程序总迭代次数为10000次,有效迭代次数为89次,最后一次有效迭代出现在第3637次。与目前已知最优解误差0.16%。
原文:https://www.cnblogs.com/Alex-Xu-OR/p/9493785.html