Computing probability queries in a Bayesian network
计算贝叶斯网络中的概率查询
1.基础因子操作
作业中因子的结构
phi = struct(‘var‘, [3 1 2], ‘card‘, [2 2 2], ‘val‘, ones(1, 8));
其中：var表示因子中变量的标签及顺序，card代表基数，描述了各变量的状态数量，val表示各变量取不同值时对应的概率分布，其向量长度等于prod(card)。
FactorProduct.m 计算两个因子的积
输入:
FACTORS.INPUT(1) = struct(‘var‘, [1], ‘card‘, [2], ‘val‘, [0.11, 0.89]);
FACTORS.INPUT(2) = struct(‘var‘, [2, 1], ‘card‘, [2, 2], ‘val‘, [0.59, 0.41, 0.22, 0.78]);
FACTORS.PRODUCT = FactorProduct(FACTORS.INPUT(1), FACTORS.INPUT(2));
期望输出：
FACTORS.PRODUCT = struct(‘var‘, [1, 2], ‘card‘, [2, 2], ‘val‘, [0.0649, 0.1958, 0.0451, 0.6942]);
我们知道，对贝叶斯网络而言，因子积其实就是表示贝叶斯链式法则。比如若FACTORS.INPUT(1) 表示学生的智力是否正常的分布，即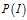
，FACTORS.INPUT(2)表示学生在其智力是否正常的条件下考试是否及格的分布，即
，则其联合概率分布可记为FACTORS.PRODUCT = FactorProduct(FACTORS.INPUT(1), FACTORS.INPUT(2))，即
。
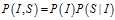计算步骤很简单，就是贝叶斯链式法则的步骤：
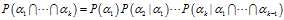
参考代码如下：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% YOUR CODE HERE:
% Correctly populate the factor values of C
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for ii = 1 : length(C.val)
C.val(ii) = A.val(indxA(ii)) * B.val(indxB(ii));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
FactorMarginalization.m 计算因子的边缘分布
输入:
FACTORS.INPUT(2) = struct(‘var‘, [2, 1], ‘card‘, [2, 2], ‘val‘, [0.59, 0.41, 0.22, 0.78]);
FACTORS.MARGINALIZATION = FactorMarginalization(FACTORS.INPUT(2), [2]);
期望输出：
FACTORS.MARGINALIZATION = struct(‘var‘, [1], ‘card‘, [2], ‘val‘, [1 1]);
本质上，求边缘分布就是一个求和的过程。对相应变量的值求和就可以了。
参考代码如下：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% YOUR CODE HERE
% Correctly populate the factor values of B
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for ii = 1 : length(unique(indxB))
B.val(ii) = sum(A.val(indxB == ii));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
ObserveEvidence.m 变量观测
输入:
FACTORS.INPUT(1) = struct(‘var‘, [1], ‘card‘, [2], ‘val‘, [0.11, 0.89]);
FACTORS.INPUT(2) = struct(‘var‘, [2, 1], ‘card‘, [2, 2], ‘val‘, [0.59, 0.41, 0.22, 0.78]);
FACTORS.INPUT(3) = struct(‘var‘, [3, 2], ‘card‘, [2, 2], ‘val‘, [0.39, 0.61, 0.06, 0.94]);
FACTORS.EVIDENCE = ObserveEvidence(FACTORS.INPUT, [2 1; 3 2]);
期望输出:
FACTORS.EVIDENCE(1) = struct(‘var‘, [1], ‘card‘, [2], ‘val‘, [0.11, 0.89]);
FACTORS.EVIDENCE(2) = struct(‘var‘, [2, 1], ‘card‘, [2, 2], ‘val‘, [0.59, 0, 0.22, 0]);
FACTORS.EVIDENCE(3) = struct(‘var‘, [3, 2], ‘card‘, [2, 2], ‘val‘, [0, 0.61, 0, 0]);
在ObserveEvidence函数中，第二个参数为一个
的矩阵，第一列表示所观测的变量，第二列表示对应变量的取值。要求只保留因子中被观测变量所对应取值的概率，被观测变量的其他取值对应概率置0。未被观测变量不受影响。
参考代码如下：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% YOUR CODE HERE
% Adjust the factor F(j) to account for observed evidence
% Hint: You might find it helpful to use IndexToAssignment
% and SetValueOfAssignment
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
assignments = IndexToAssignment(1 : length(F(j).val), F(j).card);
F(j).val(assignments(:, indx) ~= x) = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
2.计算联合分布
ComputeJointDistribution.m 计算贝叶斯网络的联合概率分布
输入:
FACTORS.INPUT(1) = struct(‘var‘, [1], ‘card‘, [2], ‘val‘, [0.11, 0.89]);
FACTORS.INPUT(2) = struct(‘var‘, [2, 1], ‘card‘, [2, 2], ‘val‘, [0.59, 0.41, 0.22, 0.78]);
FACTORS.INPUT(3) = struct(‘var‘, [3, 2], ‘card‘, [2, 2], ‘val‘, [0.39, 0.61, 0.06, 0.94]);
FACTORS.JOINT = ComputeJointDistribution(FACTORS.INPUT);
期望输出:
FACTORS.JOINT = struct(‘var‘, [1, 2, 3], ‘card‘, [2, 2, 2], ‘val‘, [0.025311, 0.076362, 0.002706, 0.041652, 0.039589, 0.119438, 0.042394, 0.652548]);
如前所述，在贝叶斯网络中，联合概率分布就是其因子积。下面是不同的表述：
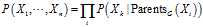
参考代码如下：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% YOUR CODE HERE:
% Compute the joint distribution defined by F
% You may assume that you are given legal CPDs so no input checking is required.
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Joint = F(1);
for ii = 2 : length(F)
Joint = FactorProduct(Joint, F(ii));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
3.计算边缘分布
ComputeMarginal.m 计算贝叶斯网络的边缘概率分布
输入:
FACTORS.INPUT(1) = struct(‘var‘, [1], ‘card‘, [2], ‘val‘, [0.11, 0.89]);
FACTORS.INPUT(2) = struct(‘var‘, [2, 1], ‘card‘, [2, 2], ‘val‘, [0.59, 0.41, 0.22, 0.78]);
FACTORS.INPUT(3) = struct(‘var‘, [3, 2], ‘card‘, [2, 2], ‘val‘, [0.39, 0.61, 0.06, 0.94]);
FACTORS.MARGINAL = ComputeMarginal([2, 3], FACTORS.INPUT, [1, 2]);
期望输出:
FACTORS.MARGINAL = struct(‘var‘, [2, 3], ‘card‘, [2, 2], ‘val‘, [0.0858, 0.0468, 0.1342, 0.7332]);
相比之前计算因子的边缘分布，这里主要多了归一化的要求，同时还要注意合并相同变量的问题。
参考代码如下：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% YOUR CODE HERE:
% M should be a factor
% Remember to renormalize the entries of M!
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Joint = ComputeJointDistribution(F);
M = FactorMarginalization(ObserveEvidence(Joint, E), setdiff(Joint.var, V));
M.val = M.val ./ sum(M.val);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
var：表示变量的名称及它们之间的关系，这里（‘var‘, [3,1]）表示因子描述的是phenotypeVar = 3的性状对genotypeVar = 1的基因型的条件概率分布。
card：是基数（cardinalities）的缩写，描述了元素间一一对应的集合（可能的）
Coursera概率图模型（Probabilistic Graphical Models）第一周编程作业分析
原文：https://www.cnblogs.com/polaris-shi/p/9498750.html