Special Solutions:
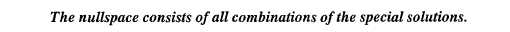

Notice what is special about s 1 and S2. They have ones and zeros in the last two components. Those components are "free" and we choose them specially. Then the first components -2 and -3 are determined by the equation Ax = 0. The first component is pivot, so it is not free. Special solutions come from our special choices.

A has rank=2, and the number of unknowns n=2, so the the number of free variables=n-r=0. Thus, no special solutions! What‘s more, A is invertible! B also doesn‘t have special solutions. But C has 2 special solutions.
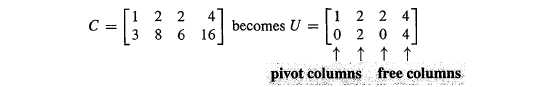
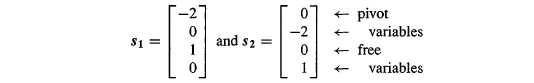
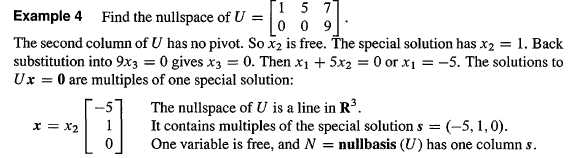
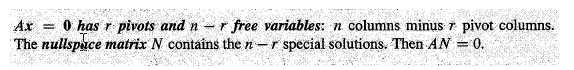
Rank:The numbers m and n give the size of a matrix-but not necessarily the true size of a linear system. An equation like 0 = 0 should not count, they can go up when elimination. The true size of A is given by its rank.
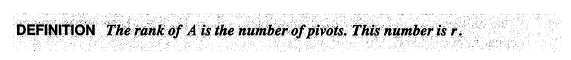


RREF(Reduced Row Echelon Form):

【读书笔记】:MIT线性代数(3):Special Solution, Rank and RREF
原文:https://www.cnblogs.com/rhyswang/p/9509251.html