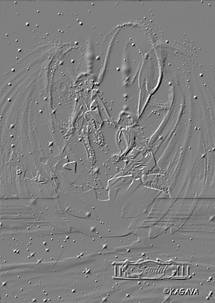
入门效果之浮雕
"浮雕"图象效果是指图像的前景前向凸出背景。常见于一些纪念碑的雕刻上,要实现浮雕其实非常简单。我们把图象的一个象素和左上方的象素进行求差运算,并加上一个灰度。这个灰度就是表示背景颜色。这里我们设置这个插值为128 (图象RGB的值是0-255)。同时,我们还应该把这两个颜色的差值转换为亮度信息.否则浮雕图像会出现彩色。
"precision mediump float; \n"
"varying vec2 v_texCoord; \n"
"uniform sampler2D s_baseMap; \n"
"uniform vec2 TexSize; \n"
"void main() \n"
"{ \n"
" vec2 tex =v_texCoord; \n"
" vec2 upLeftUV = vec2(tex.x-1.0/TexSize.x,tex.y-1.0/TexSize.y); \n"
" vec4 curColor = texture2D(s_baseMap,v_texCoord); \n"
" vec4 upLeftColor = texture2D(s_baseMap,upLeftUV); \n"
" vec4 delColor = curColor - upLeftColor; \n"
" float h = 0.3*delColor.x + 0.59*delColor.y + 0.11*delColor.z; \n"
" vec4 bkColor = vec4(0.5, 0.5, 0.5, 1.0); \n"
" gl_FragColor = vec4(h,h,h,0.0) +bkColor; \n"
"} \n";
入门效果之马赛克
接下来我们完成一个更加常见的效果—马赛克.图片的马赛克就是把图片的一个相当大小的区域用同一个点的颜色来表示.可以认为是大规模的降低图像的分辨率,而让图像的一些细节隐藏起来, 比如电视中要秀一下某个罪犯的身材,却又不能展示他的脸,这个时候我们就可以给他的脸加一个马赛克.
用HLSL代码实现马赛克是非常简单的,但是同样的,我们需要一些额外的步骤,第一步就是先把纹理坐标转换成图像实际大小的整数坐标.接下来,我们要把图像这个坐标量化---比如马赛克块的大小是8x8象素。那么我们可以用下列方法来得到马赛克后的图像采样值,假设[x.y]为图像的整数坐标:
[x,y]mosaic = [ int(x/8)*8 , int(y/8)*8].
"precision mediump float; \n"
"varying vec2 v_texCoord; \n"
"uniform sampler2D s_baseMap;\n"
"uniform vec2 TexSize; \n"
"vec2 mosaicSize = vec2(8,8);\n"
"void main() \n"
"{ \n"
" vec2 intXY = vec2(v_texCoord.x*TexSize.x, v_texCoord.y*TexSize.y); \n"
" vec2 XYMosaic = vec2(floor(intXY.x/mosaicSize.x)*mosaicSize.x,floor(intXY.y/mosaicSize.y)*mosaicSize.y); \n"
" vec2 UVMosaic = vec2(XYMosaic.x/TexSize.x,XYMosaic.y/TexSize.y); \n"
" vec4 baseMap = texture2D(s_baseMap,UVMosaic); \n"
" gl_FragColor = baseMap; \n"
"} \n";
读者可能会发现这个马赛克太普通了,确实它不够新颖,下面我们来改良一下,我们希望达到这样一个效果:马赛克区域不是方的,而是圆的,圆形区域以外,我们用图像原来的颜色覆盖。这样我们需要改变一下代码。
首先求出原来马赛克区域的正中心(原来是左上角):然后计算图像采样点到这个中心的距离,如果在马赛克圆内,就用区域的中心颜色,否则就用原来的颜色。改良后的代码如下,这里我们把马赛克区域大小调节成16x16。这样效果更明显。
"precision highp float; \n"
"varying vec2 v_texCoord; \n"
"uniform sampler2D s_baseMap; \n"
"uniform vec2 TexSize; \n"
"vec2 mosaicSize = vec2(8,8); \n"
"void main() \n"
"{ \n"
" vec2 intXY = vec2(v_texCoord.x*TexSize.x, v_texCoord.y*TexSize.y); \n"
" vec2 XYMosaic = vec2(floor(intXY.x/mosaicSize.x)*mosaicSize.x,floor(intXY.y/mosaicSize.y)*mosaicSize.y) + 0.5*mosaicSize; \n"
" vec2 delXY = XYMosaic - intXY; \n"
" float delL = length(delXY); \n"
" vec2 UVMosaic = vec2(XYMosaic.x/TexSize.x,XYMosaic.y/TexSize.y); \n"
" vec4 _finalColor; \n"
" if(delL< 0.5*mosaicSize.x) \n"
" _finalColor = texture2D(s_baseMap,UVMosaic); \n"
" else \n"
" _finalColor = texture2D(s_baseMap,v_texCoord); \n"
" gl_FragColor = _finalColor; \n"
"} \n" ;
图: 改良后的马赛克效果
l 进阶效果之锐化模糊
以上两个效果相对比较简单,姑且称之为入门效果, 它并没有用到太多数字图像处理或者信号处理方面的知识。接下来我们要介绍稍微复杂一点的效果,第一个就是图像的模糊和锐化。
图像的模糊又成为图像的平滑(smoothing),我们知道人眼对高频成分是非常敏感的,如果在一个亮度连续变化的图像中,突然出现一个亮点,那么我们很容易察觉出来,类似的,如果图像有个突然的跳跃—明显的边缘,我们也是很容易察觉出来的。这些突然变化的分量就是图像的高频成分。人眼通常是通过低频成分来辨别轮廓,通过高频成分来感知细节的(这也是为什么照片分辨率低的时候,人们只能辨认出照片的大概轮廓,而看不到细节)。但是这些高频成分通常也包含了噪声成分。图像的平滑处理就是滤除图像的高频成分。
那么如何才能滤除图像的高频成分呢?我们先来介绍一下图像数字滤波器的概念。
简单通俗的来说,图像的数字滤波器其实就是一个n x n的数组(数组中的元素成为滤波器的系数或者滤波器的权重,n称为滤波器的阶)。对图像做滤波的时候,把某个像素为中心的nxn个像素的值和这个滤波器做卷积运算(也就是对应位置上的像素和对应位置上的权重的乘积累加起来),公式如下

通常情况下,我们滤波器的阶数为3已经足够了,用于模糊处理的3x3滤波器如下

"precision mediump float; \n"
"vec4 dip_filter(mat3 _filter, sampler2D _image, vec2 _xy, vec2 texSize) \n"
"{ \n"
" mat3 _filter_pos_delta_x=mat3(vec3(-1.0, 0.0, 1.0), vec3(0.0, 0.0 ,1.0) ,vec3(1.0,0.0,1.0)); \n"
" mat3 _filter_pos_delta_y=mat3(vec3(-1.0,-1.0,-1.0),vec3(-1.0,0.0,0.0),vec3(-1.0,1.0,1.0)); \n"
" vec4 final_color = vec4(0.0, 0.0, 0.0, 0.0); \n"
" for(int i = 0; i<3; i++) \n"
" { \n"
" for(int j = 0; j<3; j++) \n"
" { \n"
" vec2 _xy_new = vec2(_xy.x + _filter_pos_delta_x[i][j], _xy.y + _filter_pos_delta_y[i][j]); \n"
" vec2 _uv_new = vec2(_xy_new.x/texSize.x, _xy_new.y/texSize.y); \n"
" final_color += texture2D(_image,_uv_new) * _filter[i][j]; \n"
" } \n"
" } \n"
" return final_color; \n"
"} \n"
"varying vec2 v_texCoord; \n"
"uniform vec2 TexSize; \n"
"uniform sampler2D s_baseMap; \n"
"void main() \n"
"{ \n"
" vec2 intXY = vec2(v_texCoord.x * TexSize.x, v_texCoord.y * TexSize.y); \n"
" mat3 _smooth_fil = mat3(1.0/9.0,1.0/9.0,1.0/9.0, \n"
" 1.0/9.0,1.0/9.0,1.0/9.0, \n"
" 1.0/9.0,1.0/9.0,1.0/9.0); \n"
" vec4 tmp = dip_filter(_smooth_fil, s_baseMap, intXY, TexSize);"
" gl_FragColor = tmp; \n"
"} \n";
以上的模糊滤波器称为BOX滤波器,是最简单的滤波器,如果考虑到离开中心像素的距离对滤波器系数的影响,我们通常采用更加合理的滤波器---高斯滤波器—一种通过2维高斯采样得到的滤波器,它的模板如下:
很容易看出来,离开中心越远的像素,权重系数越小。
对于锐化操作,常用的锐化模板是拉普拉斯(Laplacian)模板,这个模板定义如下:
容易看出拉普拉斯模板的作法:先将自身与周围的8个象素相减,表示自身与周围象素的差别;再将这个差别加上自身作为新象素的灰度。可见,如果一片暗区出现了一个亮点,那么锐化处理的结果是这个亮点变得更亮,这就增强了图像的细节。
下面三副图分别表示了经过BOX滤波。高斯滤波和拉普拉斯滤波后的图像



BOX 模糊 高斯模糊 拉普拉斯锐化
高斯模糊和拉普拉斯锐化效果的GLSL和BOX的代码基本一致,就是filter的系数不同,这里不在列出。
通过这个两个效果,我们介绍了图像的滤波操作,这样的操作,也成为模板操作,它实现了一种邻域运算(Neighborhood Operation),即某个象素点的结果灰度不仅和该象素灰度有关,而且和其邻域点的值有关。模板运算在图象处理中经常要用到,可以看出,它是一项非常耗时的运算。有一种优化的方法称为可分离式滤波,就是使用两个pass来进行x/y方向分别滤波,能让运算次数大大减少。而且滤波器阶数越高,优势越明显。
数字图像滤波的时候,同样还需要注意边界像素的问题,不过幸好,GLSL能让边界处理更加的透明和简单。
l 进阶效果之描边效果
相对浮雕效果来说,描边(边缘检测)的代码并不复杂多少,只是在理论上相对来说稍微复杂一点,而且效果看上去更加的讨人喜欢一些。
我们知道 ,如果在图像的边缘处,灰度值肯定经过一个跳跃,我们可以计算出这个跳跃,并对这个值进行一些处理,来得到边缘浓黑的描边效果。
首先我们可以考虑对这个象素的左右两个象素进行差值,得到一个差量,这个差量越大,表示图像越处于边缘,而且这个边缘应该左右方向的,同样我们能得到上下方向和两个对角线上的图像边缘。这样我们构造一个滤波器
经过这个滤波器后,我们得到的是图像在这个象素处的变化差值,我们把它转化成灰度值,并求绝对值(差值可能为负),然后我们定义差值的绝对值越大的地方越黑(边缘显然是黑的),否则越白,我们便得到如下的效果:

图:铅笔描边效果
该效果的代码如下(其中dip_filter函数代码同上):
"precision mediump float; \n"
"vec4 dip_filter(mat3 _filter, sampler2D _image, vec2 _xy, vec2 texSize) \n"
"{ \n"
" mat3 _filter_pos_delta_x=mat3(vec3(-1.0, 0.0, 1.0), vec3(0.0, 0.0 ,1.0) ,vec3(1.0,0.0,1.0)); \n"
" mat3 _filter_pos_delta_y=mat3(vec3(-1.0,-1.0,-1.0),vec3(-1.0,0.0,0.0),vec3(-1.0,1.0,1.0)); \n"
" vec4 final_color = vec4(0.0, 0.0, 0.0, 0.0); \n"
" for(int i = 0; i<3; i++) \n"
" { \n"
" for(int j = 0; j<3; j++) \n"
" { \n"
" vec2 _xy_new = vec2(_xy.x + _filter_pos_delta_x[i][j], _xy.y + _filter_pos_delta_y[i][j]); \n"
" vec2 _uv_new = vec2(_xy_new.x/texSize.x, _xy_new.y/texSize.y); \n"
" final_color += texture2D(_image,_uv_new) * _filter[i][j]; \n"
" } \n"
" } \n"
" return final_color; \n"
"} \n"
"varying vec2 v_texCoord; \n"
"uniform vec2 TexSize; \n"
"uniform sampler2D s_baseMap; \n"
"void main() \n"
"{ \n"
" vec2 intXY = vec2(v_texCoord.x * TexSize.x, v_texCoord.y * TexSize.y); \n"
" mat3 _smooth_fil = mat3(-0.5,-1.0,0.0, \n"
" -1.0,0.0,1.0, \n"
" 0.0,1.0,0.5); \n"
" vec4 delColor = dip_filter(_smooth_fil, s_baseMap, intXY, TexSize); \n"
" float deltaGray = 0.3*delColor.x + 0.59*delColor.y + 0.11*delColor.z; \n"
" if(deltaGray < 0.0) deltaGray = -1.0 * deltaGray; \n"
" deltaGray = 1.0 - deltaGray; \n"
" gl_FragColor = vec4(deltaGray,deltaGray,deltaGray,1.0); \n"
"} \n";上面演示的效果种用到的模板就是一种边缘检测器,在信号处理上是一种基于梯度的滤波器,又称边缘算子,梯度是有方向的,和边沿的方向总是正交(垂直)的,在上面的代码中,我们采用的就是一个梯度为45度方向模板,它可以检测出135度方向的边沿。
以上是简单的边缘检测算子,更加严格的,我们可以采样Sobel算子,Sobel 算子有两个,一个是检测水平边沿的 



l 高级效果之伪 HDR/Blow
HDR和Blow在现在主流游戏中是非常时髦的效果。
所谓HDR就是高动态范围的意思,我们知道,在普通的显示器和位图里,每通道都是8-bit,也就是说RGB分量的范围都是0-255,这用来表示现实中的颜色显然是远远不够的,现实中的图像的动态范围远远大的多,那么如何在现有的显示设备里尽可能的保持更大的动态范围,而且让它能更符合人眼的习惯就成了图形学研究的一个热点。通常真正的HDR的做法都是采用浮点纹理,把渲染运算的过程中,我们使用16bit的动态范围来保存运算结果,然后我们对运算结果进行分析,求出这个图像的中间灰度值,然后对图像进行调整映射到LDR的设备中。但是这样的算法有两个非常耗资源的过程,其中一个是浮点纹理,另外一个就是求图像中间灰度(通常情况是把图像不停的渲染到RenderTarget,每渲染一次,图像大小缩小一半,直到缩小到1x1大,一个1024 x1024的图像需要渲染10次!)。因此虽然HDR的效果非常漂亮,但是目前还是只有为数不多的游戏采用了这样的算法,大部分都是采用的伪HDR+blow效果。
伪HDR效果通常是重新调整图像的亮度曲线,让亮的更亮,暗的更暗一些,而Blow效果则是图像的亮度扩散开来,产生很柔的效果。
在这里我们采用一个二次曲线来重新调整图像的亮度,这个曲线的方程是
x [ (2-4k) x + 4k-1 ).
K的取值范围为0.5 – 2.0
经过这个公式调整以后,图像上亮的区域将更加的亮,并且整体亮度会提高。那么接下来,我们如何使图像的亮度扩散开来呢?一种可行的方法就是对场景图像做一次downsample。把它变成原来的1/4次大小,那样就等于亮度往外扩散了4x4个象素的区域。
"precision mediump float; \n"
"varying vec2 v_texCoord; \n"
"uniform sampler2D s_baseMap; \n"
"uniform float k; \n"
"vec4 xposure(vec4 _color, float gray, float ex) \n"
"{ \n"
" float b = (4.0*ex - 1.0); \n"
" float a = 1.0 - b; \n"
" float f = gray*(a*gray + b); \n"
" return f*_color; \n"
"} \n"
"void main() \n"
"{ \n"
" vec4 _dsColor = texture2D(s_baseMap, v_texCoord); \n"
" float _lum = 0.3*_dsColor.x + 0.59*_dsColor.y; \n"
" vec4 _fColor = texture2D(s_baseMap, v_texCoord); \n"
" gl_FragColor = xposure(_fColor, _lum, k); \n"
"} \n";下面是原图像和经过处理后图像的对比:



原图 k = 1.1 k = 1.6
图:经过伪HDR+Blow处理过的图像和原图的对比
l 高级效果之水彩化
真正的水彩效果在shader中是比较难实现的,它需要进行中值滤波后累加等一些操作,还需要处理NPR中的笔触一类的概念。本文绕开这些概念,只从视觉效果上能尽量模拟出水彩的画的那种感觉来。
我们知道,水彩画一个最大的特点是水彩在纸上流动扩散后会和周围的颜色搅拌在一起,另外一个特点就是水彩通常会形成一个个的色块,过渡不像照片那样的平滑。针对这两个特点。我们可以设计这样的一个算法来模拟水彩画的效果。
我们可以采用噪声纹理的方式,既事先计算好一个nxn的随机数数组,作为纹理传递给Pixel shader,这样在Pixel Shader里我们就能获得随机数了。得到随机数后,我们将随机数映射成纹理坐标的偏移值,就能模拟出色彩的扩散了。典型的噪声纹理是这个样子的:
图:噪声纹理
接下来我们需要处理色块,我们对颜色的RGB值分别进行量化,把RGB分量由原来的8bit量化成比特数更低的值。这样颜色的过渡就会显得不那么的平滑,而是会呈现出一定的色块效果。
通过以上两步处理后,我们得到的图像依然有非常多的细节,尤其是第一步处理中产生的很多细节噪点,很自然的我们就想到通过平滑模糊的方式来过滤掉这些高频噪声成分。
算法设计好了,接下来看看我们如何在RenderMonkey里实现这个算法。
类似上一个效果,我们需要两个pass来完成这个算法,第一个pass叫flow pass,模拟颜色的流动和处理颜色的量化。第二个pass叫Gauss pass,也就是前面提到的高斯模糊算法。我们的重点在第一个pass。
在模拟扩散的pass中,我们同样需要一个RenderTarget,以把结果保存在其中以便后续处理,然后还需要一个噪声纹理来产生随机数。具体代码如下:
"precision mediump float; \n"
"varying vec2 v_texCoord; \n"
"uniform sampler2D s_baseMap; \n"
"uniform vec2 TexSize; \n"
"float _waterPower = 40.0; \n"
"float _quatLevel = 5.0; \n"
"vec4 quant(vec4 _cl, float n) \n"
"{ \n"
" _cl.x = floor(_cl.x*255.0/n)*n/255.0; \n"
" _cl.y = floor(_cl.y*255.0/n)*n/255.0; \n"
" _cl.z = floor(_cl.z*255.0/n)*n/255.0; \n"
" return _cl; \n"
"} \n"
"void main() \n"
"{ \n"
" vec4 noiseColor = _waterPower*texture2D(s_baseMap,v_texCoord); \n"
" vec2 newUV =vec2 (v_texCoord.x + noiseColor.x/TexSize.x,v_texCoord.y + noiseColor.y/TexSize.y); \n"
" vec4 _fColor = texture2D(s_baseMap,newUV); \n"
" gl_FragColor = quant(_fColor, 255.0/pow(2,_quatLevel)); \n"
"} \n";代码中的_quatLevel用来表示对图像的量化比特数,值越小,色块越明显,比较合理的取值范围是2-6。_waterPower则表示图像颜色扩散范围,取值范围在8-64之间的效果比较好。
下面是经过水彩画处理后的图像:


图:水彩画效果。左图量化比特数为6比特,扩散范围为20象素。
右图量化比特数为5比特,扩散范围为40象素
原文:http://blog.csdn.net/neng18/article/details/38083987