在一个无向图中,若任意两点间至少存在两条“点不重复”的路径,则说这个图是点双连通的(简称双连通,biconnected)
在一个无向图中,点双连通的极大子图称为点双连通分量(简称双连通分量,Biconnected Component,BCC)
在Tarjan过程中维护一个栈,每次Tarjan到一个结点就将该结点入栈,回溯时若目标结点low值不小于当前结点dfn值(找到一个BCC)就出栈直到当前结点(当前结点属于该BCC但不出栈)
(说实话我觉得存点不比存边难理解而且实现快啊……下面会解释)
首先申明一下,在我找到的BCC资料中,在算法实现中均将两个点和一条边构成的图称为BCC,此文章也沿用此的规定
如下图:

我猜想可能是因为割点的定义,此图中两个点均不为割点,所以此图也属于BCC?
总之做题时注意题面要求,若要求的不含此种BCC则判断每个BCC的大小即可
无向连通图中割点一定属于至少两个BCC,非割点只属于一个BCC
有了上面的定义我们也不难理解这一条了:割点就算相邻也会属于至少两个BCC;BCC间的交点都是割点,所以非割点只属于一个BCC
回溯时若目标结点low值不小于当前结点dfn值就出栈直到当前结点(当前结点属于该BCC但不出栈)
一、当前结点为自下到上第一个(即高度最小的)割点
因为此结点是自下到上第一个,所以一定有至少一个孩子的low值=当前结点的dfn值
这个可以用反证法证明一下
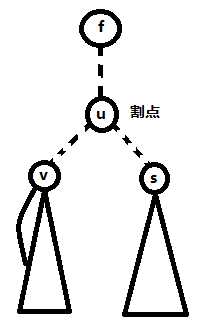
low[v]=dfn[v]>dfn[u],那么v也是割点,这样u就不是高度最小的割点
所以满足条件的子树与割点构成一个双连通分量
二、当前结点为非根节点且不满足(一)
此部分BCC一定存在于割点之间
由于算法中的出栈操作已经将所有子树中最近(高度最高)的割点以下的结点全部出栈,所以我们直接进行算法中的出栈操作即都是割点间的结点(包括割点)
三、当前结点为根结点
1、当前结点只有一个子树,即当前结点不是割点,显然当前结点属于其孩子所在BCC
2、当前结点有多于一个子树,即当前结点是割点,则当前结点是其各个孩子所在BCC的交点,算法的正确性也很显然
综上,存点是不是很好理解?存边虽然不会涉及重复问题(割点属于至少两个BCC),但会有很多无用操作,写起来也稍麻烦些
并没有模板题

1 #include<cstdio> 2 #include<cctype> 3 #include<vector> 4 #include<stack> 5 using namespace std; 6 struct edge 7 { 8 int to,pre; 9 }edges[1000001]; 10 int head[1000001],dfn[1000001],dfs_clock,tot; 11 int num;//BCC数量 12 stack<int>s; 13 vector<int>bcc[1000001]; 14 int read() 15 { 16 int f=0,x=0; 17 char c=getchar(); 18 while(!isdigit(c)) 19 { 20 f=f|c==‘-‘; 21 c=getchar(); 22 } 23 while(isdigit(c)) 24 { 25 x=(x<<1)+(x<<3)+(c^48); 26 c=getchar(); 27 } 28 return x; 29 } 30 int tarjan(int u,int fa) 31 { 32 int lowu=dfn[u]=++dfs_clock; 33 for(int i=head[u];i;i=edges[i].pre) 34 if(!dfn[edges[i].to]) 35 { 36 s.push(edges[i].to);//搜索到的边入栈 37 int lowv=tarjan(edges[i].to,u); 38 lowu=min(lowu,lowv); 39 if(lowv>=dfn[u])//是割点或根 40 { 41 num++; 42 while(s.top()!=u)//将边出栈直到当前边 43 { 44 bcc[num].push_back(s.top()); 45 s.pop(); 46 } 47 bcc[num].push_back(u); 48 } 49 } 50 else if(edges[i].to!=fa) 51 lowu=min(lowu,dfn[edges[i].to]); 52 return lowu; 53 } 54 void add(int x,int y)//邻接表存边 55 { 56 edges[++tot].to=y; 57 edges[tot].pre=head[x]; 58 head[x]=tot; 59 } 60 int main() 61 { 62 int n,m; 63 scanf("%d%d",&n,&m); 64 for(int i=1;i<=m;i++) 65 { 66 int x,y; 67 scanf("%d%d",&x,&y); 68 add(x,y),add(y,x); 69 } 70 for(int i=1;i<=n;i++)//遍历n个点tarjan 71 if(!dfn[i]) 72 { 73 s.push(i); 74 tarjan(i,i); 75 } 76 for(int i=1;i<=num;i++) 77 { 78 printf("BCC%d: ",i); 79 for(int j=0;j<bcc[i].size();j++) 80 printf("%d ",bcc[i][j]); 81 printf("\n"); 82 } 83 return 0; 84 }
原文:https://www.cnblogs.com/LiHaozhe/p/9527136.html