给你多组数据集，例如给你很多房子的面积、房子距离市中心的距离、房子的价格，然后再给你一组面积、 距离，让你预测房价。这类问题称为回归问题。
回归问题（Regression) 是给定多个自变量、一个因变量以及代表它们之间关系的一些训练样本，来确定它们的关系。其中最简单的一类是线性回归（Linear Degression）。
线性回归函数的形式如下:
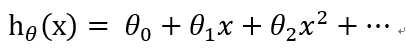（1）
θj 是我们要求的系数。接下来介绍一下求θ 的两种方法，梯度下降（Gradient Descent）和正规方程（Normal Rquation )。
1. 梯度下降法
描述：梯度下降法（Gradient descent）是一个一阶最优化算法，通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点；这个过程则被称为梯度上升法。
公式：
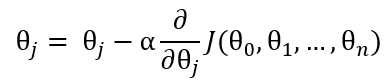（2）
其中，J(θ) 称为代价函数(Cost Function )或损失函数(Loss Function), 用来量度预测结果和标准结果之间的误差，常见的有交叉熵，均方误差，平均绝对值误差等。在这里使用均方误差。α是学习速率，取值自定，一般取比较小的数，如0.0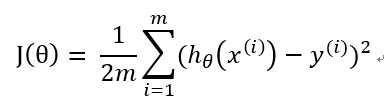3
（3）
( hθ(x) 是x经过待求的函数得出的结果，y(i) 是数据集中的结果)
公式（2）的旨在求出最小的θj，把代价函数J(θ)降到最小。它的原理是θ不停地迭代，减去θ对应的代价函数在x的偏导，如果偏导是正的，那么J(θ)在该方向单增，减去这个正数后θ变小，J(θ)也会跟着变小；反之，如果偏导是负的，J(θ)单减，原θ减负数，θ变大，J(θ)减小。无论怎样,J(θ)都朝着减小的方向变化。值得注意的是，如果学习速率α偏大，那么θ在做差的话可能减过头甚至得到的新J(θ)比原来还要大,而如果学习速率α偏小，那么花费的时间会变长。
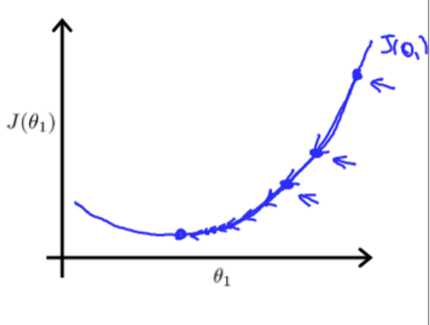（结合图像更直观）
梯度下降算法是一个不断迭代的过程，需要不断重复公式（2），直到J(θ)符合预期误差或者达到足够的迭代次数。
具体步骤如下：
step0: 初始化α，θ（任意值）和迭代次数；
step1:利用公式（3） ，求J(θ）;
step2:利用公式（2），本次迭代的新θ;
step3:重复step1 - step2
2. 正规方程
利用正规方程可以直接计算计算θ，前提是(XTX)必须可逆
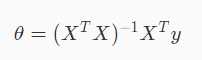
3. matlab实现
3.1 初始化参数
data = load(‘ex1data1.txt‘); X = data(:, 1); y = data(:, 2); m = length(y); % number of training examples plotData(X, y) X = [ones(m, 1), data(:,1)]; % Add a column of ones to x theta = zeros(2, 1); % initialize fitting parameters % Some gradient descent settings iterations = 1500; alpha = 0.01;
3.2 计算代价函数
3.3 梯度下降并迭代
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters) %GRADIENTDESCENT Performs gradient descent to learn theta % theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by % taking num_iters gradient steps with learning rate alpha % Initialize some useful values m = length(y); % number of training examples J_history = zeros(num_iters, 1); x = X(:,2); for iter = 1:num_iters % ====================== YOUR CODE HERE ====================== % Instructions: Perform a single gradient step on the parameter vector % theta. % % Hint: While debugging, it can be useful to print out the values % of the cost function (computeCost) and gradient here. % J = alpha * (1/m) * (X * theta - y)‘ ; theta(1) = theta(1) - J * ones(m,1); theta(2) = theta(2) - J * x; % ============================================================ % Save the cost J in every iteration J_history(iter) = computeCost(X, y, theta); end end
3.4 绘图
% Grid over which we will calculate J theta0_vals = linspace(-10, 10, 100); theta1_vals = linspace(-1, 4, 100); % initialize J_vals to a matrix of 0‘s J_vals = zeros(length(theta0_vals), length(theta1_vals)); % Fill out J_vals for i = 1:length(theta0_vals) for j = 1:length(theta1_vals) t = [theta0_vals(i); theta1_vals(j)]; J_vals(i,j) = computeCost(X, y, t); end end % Because of the way meshgrids work in the surf command, we need to % transpose J_vals before calling surf, or else the axes will be flipped J_vals = J_vals‘; % Surface plot figure; surf(theta0_vals, theta1_vals, J_vals) xlabel(‘\theta_0‘); ylabel(‘\theta_1‘); % Contour plot figure; % Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100 contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20)) xlabel(‘\theta_0‘); ylabel(‘\theta_1‘); hold on; plot(theta(1), theta(2), ‘rx‘, ‘MarkerSize‘, 10, ‘LineWidth‘, 2);
原文：https://www.cnblogs.com/lvdalao/p/9520905.html