Unity中,transform有一个很有意思的方法:
TransForm.LookAt(Transform target, Vector3 WorldUp);
缺省时,
Transform.LookAt(Transform target);
这个方法可以理解成为:
1-目的是,使得自身的transform.forward指向目标对象
2-将自身以世界坐标的transform.up为转动轴,rotate,使得1得以实现
好比是一个人的身子绕头顶--脚心的轴转动,让自己的眼镜,看着对象。
方法很简洁实用。然而有局限性,主要在于转动轴上。设想如下一个问题:一个斜坡上有一辆坦克,需要转动炮塔,对准并不在这个斜坡上的一个物体。
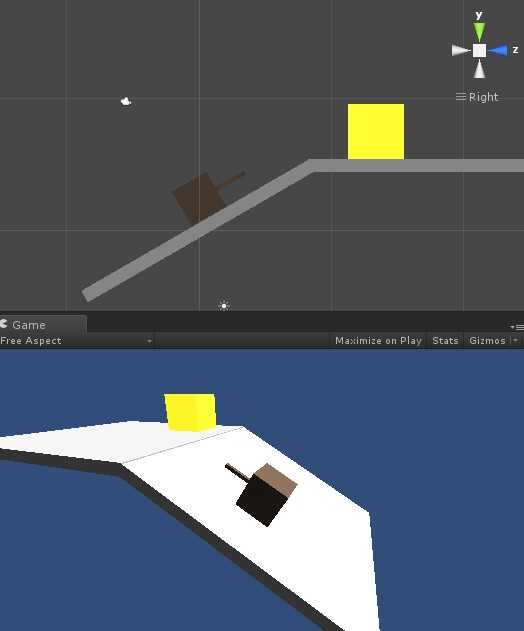
上方侧视图中示意了坦克在斜面上,黄色物体在上方的水平面上。下方的透视图中,可以看到这二者的空间位置关系。
我们希望坦克用炮管对准这个黄色物体,这里的对准,其实是平面对准,让炮管的指向在坦克和物体构成的平面中。
示意一下,这个效果:
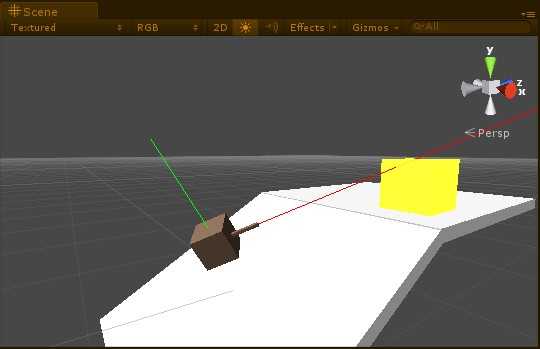
坦克旋转了,炮管指向了物体,并且这个旋转,使得坦克的transform.up方向还是垂直于所在的斜面。
先简单用LookAt来试试?
void Update () { transform.LookAt(target.transform); Debug.DrawRay(transform.position,10f*transform.forward,Color.red); Debug.DrawRay(transform.position,3f*transform.up,Color.green); }
在Update中不断更新这个tranform.LookAt(),我们得到的是这样一个效果:炮管指向了物体,但是坦克旋转的轴向,并不是transform.up,而是WorldUp,显然,坦克翘起了脚,脱离了所在的斜面。
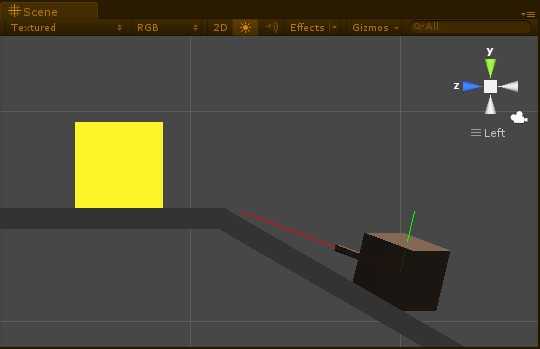
不能用简单的LookAt来实现,于是回归到基础的分析:
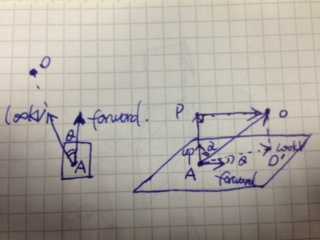
如果物体O,在坦克的水平面上,也就是图左所示。那么问题比较简单,向量AO就是向量forward需要转到的最终方向lookV,计算一下两者的夹角,按照A.transform.up作为旋转轴,旋转这个角度;至于顺时针还是逆时针,取决于两个向量的叉乘(另文已述)。
如果物体O,不在坦克的水平面上,如图右所示。A的旋转轴只能是A.transform.up,因此A的lookV,是向量AO‘,这个 O’ 是O在坦克水平面上的投影,也就是说,需要计算出AO在坦克水平面的投影向量。
查找了一些资料,关于计算向量在平面上的投影向量,最靠谱的是这个:
那么,在unity中,这样来实现它:
1-计算A.transform.up与AO的点乘, ,由于A.transform.up的模长为1,
,由于A.transform.up的模长为1,
点乘得到的结果为图右中PA的长度,可以转化为向量AP:
Vector3 projectV = Vector3.Dot(targetPos-selfPos,transform.up)*transform.up;//project to up-axis
2-AO‘就是PO’,容易得到向量AO 减去 向量AP,就可以得到
lookDir = targetPos-selfPos-projectV;
3-转化为在同一个平面中,旋转的lookV的问题了
void LookAtTarget(){ targetPos = target.transform.position; selfPos = transform.position; if(targetPos != selfPos){//targetPos == selfPos, no where to look Vector3 projectV = Vector3.Dot(targetPos-selfPos,transform.up)*transform.up;//project to up-axis lookDir = targetPos-selfPos-projectV; if(lookDir !=Vector3.zero){//lookDir == 0,target is up the head ,no where to look Vector3 crossV = Vector3.Cross(lookDir,transform.forward).normalized; if(crossV !=Vector3.zero){//crossV == 0 , target is looking at ,no need to rotate if(crossV == transform.up){ transform.Rotate(transform.up,-Vector3.Angle(lookDir,transform.forward),Space.World); } else{ transform.Rotate(transform.up,Vector3.Angle(lookDir,transform.forward),Space.World); } } } } }
另外有一些细节的问题,已经在代码中注释。
总体来说,这个方法,由于特定的轴向旋转,而不是世界坐标轴,而其中向量点乘用于计算投影向量,向量叉乘用于计算旋转的顺时针逆时针。
原文:http://www.cnblogs.com/tianiao/p/3545065.html