Tom最近在研究一个有趣的排序问题。如图所示,通过2个栈S1和S2,Tom希望借助以下4种操作实现将输入序列升序排序。
操作a
如果输入序列不为空,将第一个元素压入栈S1
操作b
如果栈S1不为空,将S1栈顶元素弹出至输出序列
操作c
如果输入序列不为空,将第一个元素压入栈S2
操作d
如果栈S2不为空,将S2栈顶元素弹出至输出序列
如果一个1~n的排列P可以通过一系列操作使得输出序列为1,2,…,(n-1),n,Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”,而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列:<a,c,c,b,a,d,d,b>
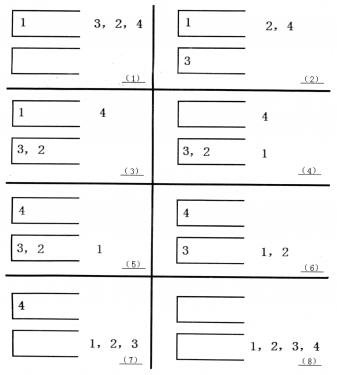
当然,这样的操作序列有可能有几个,对于上例(1,3,2,4),<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。
Solution
先考虑如何判掉不合法的情况,对于一个数,如果它前面有一个数比他大,那他们不能在同一个栈里,我们可以在它们之间连一条边,那么连出来的这张图如果有奇环,就是不合法的。
再考虑对于一个合法解,如何是答案字典序最小。
我们对于一个联通块内让编号最小的点进一号栈,那么所有元素进入栈的编号就确定了,接下来按照题意模拟,有能弹出的元素就弹出。
但这样为什么能保证字典序最小?
考虑当二号栈有元素需要弹出,下一个元素要进一号栈,那么我们应该先让一号进入,二号弹出,我们的做法就出锅了。
所以要加特判
Code
#include<iostream> #include<cstdio> #define N 1009 using namespace std; struct dd { int n,to; }an[N*N]; int a[N],co[N],head[N],tot,n,mi,p,tag,top1,top2,st1[N],st2[N]; bool vis[N]; inline void add(int u,int v) { an[++tot].n=head[u]; an[tot].to=v; head[u]=tot; } bool dfs(int u,int fa) { vis[u]=1; for(int i=head[u];i;i=an[i].n) if(an[i].to!=fa) { if(co[an[i].to]==-co[u])return 0; co[an[i].to]=-co[u]; if(!vis[an[i].to])if(!dfs(an[i].to,u))return 0; } return 1; } int main() { scanf("%d",&n); for(int i=1;i<=n;++i)scanf("%d",&a[i]); mi=0x3f3f3f3f; for(int i=n;i>=1;--i) { for(int j=1;j<i;++j) if(a[j]<a[i]&&a[j]>mi)add(j,i),add(i,j); mi=min(mi,a[i]); } for(int i=1;i<=n;++i) if(!vis[i]) { co[i]=1; if(!dfs(i,0)) { printf("0"); return 0; } } p=0; for(int i=1;i<=n;++i) { tag=co[i]==1?1:2; if(tag==1) { printf("a "); st1[++top1]=a[i]; } else { printf("c "); st2[++top2]=a[i]; } while(st1[top1]==p+1||st2[top2]==p+1) if(p+1==st1[top1])printf("b "),p++,top1--; else printf("d "),p++,top2--; } return 0; }
原文:https://www.cnblogs.com/ZH-comld/p/9550679.html